Zylinder
Volumen eines Zylinders
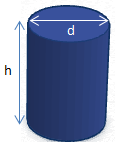
Bei einem Zylinder ist die Volumenberechnung ähnlich wie bei einem Quader. Wir berechnen die Grundfläche und multiplizieren diese anschließend mit der Höhe h. Da die Grundfläche eines Zylinders kreisförmig ist, benötigen wir die Formel für den Flächeninhalt eines Kreises. Diese lautet:
![]()
Wir haben zwei verschiedene Formeln. Eine für die Verwendung des Radius r und eine wenn wir den Durchmesser d. Für das Volumen des Zylinders müssen wir dann nur noch die Höhe h multiplizieren. Die Formel sieht also folgendermaßen aus:
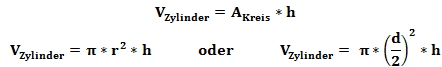
Was ist ein Zylinder?
Im Prinzip verstehen wir unter einem Zylinder nichts anderes als eine Fläche, die ausgehend von den Punkten einer festen Geraden den gleichen Abstand haben. Die feste Gerade wird als Achse bezeichnet. Wir unterscheiden in unserem Alltag und im gesamten Leben unterschiedliche Zylinder, wie zum Beispiel Münzen oder auch Türme, die sich in Ihrem Volumen, in der Mantelfläche berechnen lassen.
Die folgenden Bestandteile bilden einen Zylinder:
- Grundfläche und Deckfläche = 2 parallele, ebene Flächen
- eine Mandel bzw. Zylinderfläche – diese sind von geraden begrenzt.
So Ist der Zylinder eigentlich nichts weiter als ein geometrischer Körper, den zwei parallel zueinander liegende Kreisflächen erzeugen. Verschieben wir einen Kreis in senkrechter Ebene zur normalen, entsteht ein neuer Zylinder. Wir haben es gleich mit einer Sonderform, dem geraden Kreiszylinder, zu tun. Verschieben wir den Kreis jedoch nicht zur senkrechten, handelt es sich um einen schiefen Kreiszylinder.
Wir haben es hier mit unendlich ausgedehnten Flächen zu tun. Von daher beschneiden wir diese üblicherweise auf zwei Ebenen in einer bestimmten Distanz. Bei senkrechten Schnittebenen zur Achse sprechen wir von einem senkrechten Kreiszylinder. Die Berechnungsgrundlage bilden die unterschiedlichen Formen, die ihr alle im Tafelwerk wiederfindet.
- Die Welt der Geometrie ist frei.
- So können wir als Grundfläche nicht nur einen Kreis vorliegen haben, sondern jede beliebige andere geschlossene Kurve, wie zum Beispiel eine Ellipse.
- Ist die Grundfläche ein Viereck, haben wir es mit einem Prisma zu tun.
Was ist geometrisch besonders am Zylinder?
In einer Zylinderfläche sind Geraden enthalten. Sie bilden eine Regelfläche die sich in einer Ebene abwickeln lässt.
Die Größe des Zylinder besser verstehen
Der Radius des Kreises wird mit r abgekürzt. Die beiden Kreise begrenzen den Zylinder. So finden wir eine Grundfläche und eine Deckfläche. Den Abstand der beiden Flächen zueinander bezeichnen wir mit h. Das Besondere: Der Zylinder besitzt eine gekrümmte Mantelfläche, die wir mit M bezeichnen.
Beispiel
Wir möchten das Volumen des folgenden Zylinders berechnen:
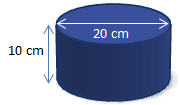
Wir haben in diesem Fall den Durchmesser d gegeben und benutzen für die Berechnung deshalb die Formel in der der Durchmesser benutzt wird. Die berechnete Einheit ist natürlich cm³, da die gegebenen Werte in cm gegeben sind.
![]()
Unser Lernvideo zu : Zylinder
Oberfläche eines Zylinders
Die Oberfläche berechnet sich indem man zunächst die einzelnen Flächen berechnet und diese dann addiert. Dafür benötigen wir zunächst die Fläche der Kreisförmigen Grundfläche. Die Formel für den Flächeninhalt eines Kreises ist bereits oben aufgeführt. Die Kreisfläche müssen wir zweimal berücksichtigen, da sich diese oben und unten befindet. Dazu kommt die Mantelfläche die sich um den Zylinder legt. Diese berechnen wir indem wir den Umfang des Grundkreises berechnen und diesen Umfang mit der Höhe des Zylinders multiplizieren. Die Formel baut sich also aus folgenden Komponenten zusammen:
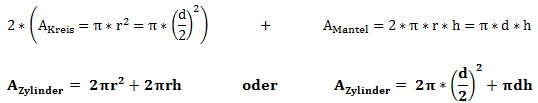
Beispiel
Berechne die Oberfläche dieses Zylinders:
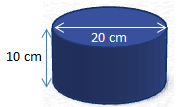
Wir entscheiden uns für die Formel in der der Durchmesser verwendet wird und setzen unsere Werte ein:
![]()
Der Oberfläche des Zylinders beträgt 1256,6 cm².
Übungsaufgaben zum Zylinder – Beispiel Littfaßsäule

Übungsaufgaben zum Zylinder – Beispiel Cremedose

