3D Koordinatensystem im Raum
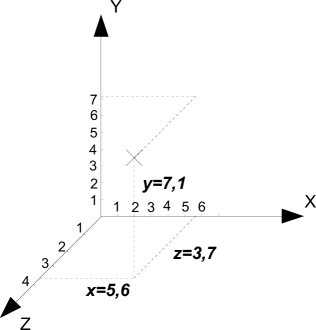
Wenn wir uns nicht nur in der Länge und Breite, sondern auch in der Höhe bewegen können, brauchen wir noch eine dritte Angabe um die Richtung zu bestimmen. Diese werden dann in ein x-y-z-Koordinatensystem eingetragen.
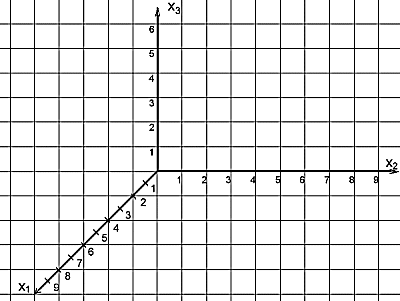
- Im 3-dimensioalen Raum R³ gibt es also drei Achsen, die x1– , die x2– und die x3– Achse
Sowohl für x1 als auch für x2 und x3 sind alle reellen Zahlen zugelassen. Mit ℝ3 ist also ein räumliches Koordinatensystem gemeint.
Wichtig ist die Angabe ℝ3 beispielsweise bei der Überprüfung der Lagebeziehung zweier Geraden. Im ℝ3 können sich Geraden nicht nur schneiden, echt parallel oder identisch sein, sondern sie können auch windschief sein, was im ℝ2 nicht möglich ist. (Anmerkung:Windschief sind Geraden, die nicht parallel sind, die sich aber auch nicht schneiden;sie laufen also „schräg“ im Raum aneinander vorbei.) Windschief können Geraden nur im dreidimensionalen Koordinatensystem, also im Raum, d.h. im ℝ3 sein!
3D koordinatensystem
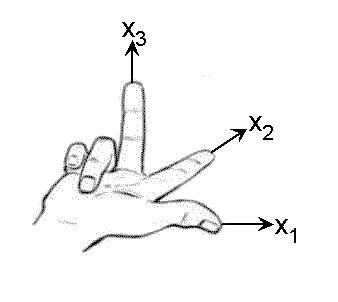
Am besten ist es, wenn Ihr euch an die Dreifingerregel orientiert! Dann kann nichts schief gehen
Die Reihenfolge der Achsen wird durch die Dreifingerregel der rechten Hand festgelegt.
Es entsteht ein rechtshändiges Koordinatensystem
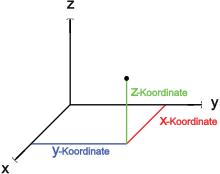
dabei sind
x3 = y-Achse
x1 =x-Achse
x2 =z-Achse
Abszisse und Ordinate
- Die x-Achse ist die horizontale Achse (von links nach rechts). Auch „Abszisse“ genannt.
- Die y-Achse ist die vertikale Achse (von oben nach unten). Auch „Ordinate“ genannt.
- Die Achsenabschnitte (also die Abstände auf den Achsen) müssen immer gleich sein.
Quadranten
Ein Koordinatensystem hat vier Quadranten
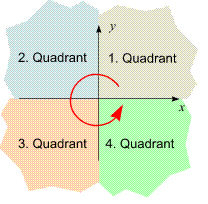
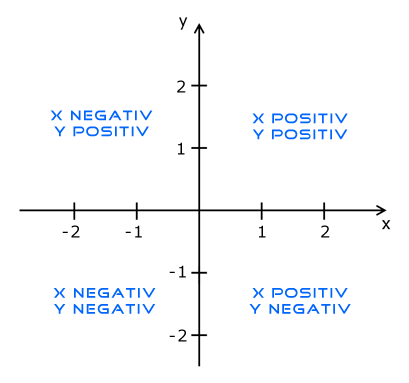
Merkt euch außerdem, dass Punkte, die auf den Achsen oder im Koordinatenursprung liegen, keinem Quadranten zugeordnet werden können. Sie haben die Koordinate/n 0 und Null ist weder positiv noch negativ, daher ist keine Zuordnung möglich.
Jeder Quadrant unterscheidet sich darin, dass die x- und y-Werte unterschiedlich positiv und negativ sind
So sieht ein 3D Koordinatensystem im Raum aus, wenn wir uns einen Punkt zeichnen