Schnittpunkt mit der x-Achse berechnen
Um die Nullstelle zu bestimmen, müssen wir die Funktion gleich 0 setzen. Wir bestimmen so den Schnittpunkt mit der x-Achse beziehungsweise den x-Wert bei y = 0. Die normale Funktionsvorschrift lautet y = a • x + b, wenn wir nun y = 0 setzen (da wir ja den x-Wert bei y = 0 ermitteln wollen) erhalten wir:
0 = a • x + b
Dies ist also die Gleichung die wir für die Nullstelle Lösen müssen. Um den x-Wert zu ermitteln lösen wir sie nach x auf:
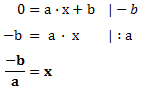
Mit dieser Formel erhalten wir die Nullstelle einer linearen Funktion.
Unser Lernvideo zu : Schnittpunkt mit der x-Achse berechnen
Beispiel
Berechne die Nullstelle von der linearen Funktion f(x) = 3 • x + 6.
Wir setzen die Funktion also als Erstes gleich 0:
![]()
Nun müssen wir die Gleichung auflösen, sodass am Ende das x auf einer Seite alleine steht. Wir ziehen also zunächst einmal die 6 auf die andere Seite indem wir auf beiden Seiten -6 rechnen.
![]()
Anschließend teilen wir durch 3, damit dann das x auf der rechten Seite alleine steht:
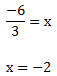
Wir wissen nun, dass die Nullstelle der Funktion bei x = -2 liegt. Um dieses Ergebnis noch einmal Grafisch zu veranschaulichen hier noch einmal die grafische Darstellung der Funktion:
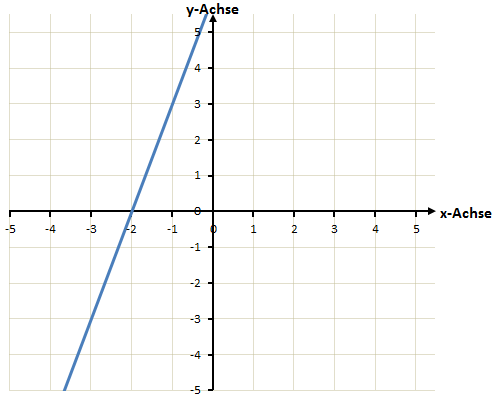
Wir sehen auch hier, dass die x-Achse bei x = -2 von der Funktion geschnitten wird.
Alternatives Vorgehen
Wir hätten natürlich auch direkt die oben hergeleitete Formel für die Nullstelle einer linearen Funktion benutzen können. Dann hätten wir a und b direkt in diese Formel eingesetzt:
![]()
Auf diese Weise wären wir schnell und einfach bei der gleichen Lösung gelandet. Ob man sich die Herleitung merkt oder jedes Mal neu durchführt ist jedem selbst überlassen.
