Kongruenzsätze
Um ein Dreieck konstruieren zu können brauchen wir bestimmte Angaben. Welche Angaben man benötigt um ein eindeutiges Dreieck zu konstruieren ist in den verschiedenen Kongruenzsätzen formuliert.
Unser Lernvideo zu : Kongruenzsätze
Kongruenzsatz: Seite Seite Seite
Wenn wir alle drei Seitenlängen eines Dreiecks gegeben haben, können wir ein Dreieck konstruieren. Das Dreieck ist damit eindeutig beschrieben. Immer wenn ein Dreieck dieselben Seitenlängen wie ein anderes aufweist, sind die beiden Dreiecke deshalb kongruent.
Beispiel
Wir haben die folgenden drei Seitenlängen gegeben:
a = 5 cm
b = 3 cm
c = 7 cm
Das Dreieck ist mit diesen Angaben genau beschrieben. Wir können also mit der Konstruktion beginnen. Als erstes zeichnen wir die erste Seite. Mit welcher wir beginnen ist egal. Wir beginnen hier mit der Seite a:
![]()
Anschließend müssen wir die beiden Seiten b und c konstruieren. Hierfür Zeichnen wir um einen Punkt einen Kreis mit dem Radius 3 cm und um den anderen Punkt einen Kreis mit dem Radius 7 cm. Anschließend markieren wir die beiden Schnittpunkte.
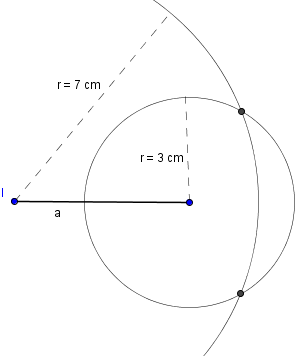
Wir müssen uns nun für den oberen oder unteren Schnittpunkt entscheiden und die beiden anderen Seiten einzeichnen. Wir haben uns in diesem Beispiel für den oberen Schnittpunkt entschieden, da die Seiten dann in der richtigen Reihenfolge (gegen den Uhrzeigersinn) sind.
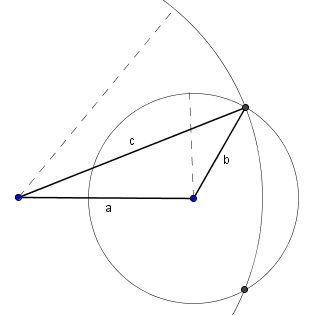
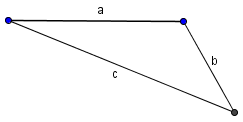
Hier noch einmal das Dreieck das wir erhalten haben. Rechts ist auch noch einmal das Dreieck abgebildet, welches wir erhalten hätten wenn wir den unteren Schnittpunkt genommen hätten. Die beiden Dreiecke sind Kongruent da man sie durch eine Spiegelung an der Seite a und einer Verschiebung ineinander überführen könnte.
Kongruenzsatz: Seite Winkel Seite
Wenn bei mehreren Dreiecken zwei Seiten und der Winkel der die beiden Seiten verbindet gleich sind, sind die Dreiecke Kongruent. Wir zeigen auch hier wie man ein Dreieck mithilfe dieser Angaben konstruieren kann.
Beispiel
Wir haben folgende Seiten und Winkle gegeben:
a = 4 cm
b = 2 cm
γ = 120°
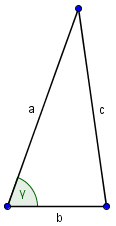
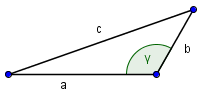
Wir schauen uns noch einmal das Standarddreieck an um zu sehen wo sich die Seiten und Winkel befinden.
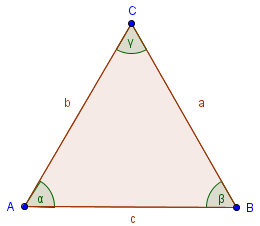
Der Winkel γ liegt zwischen den beiden Seiten a und b. Damit erfüllen unsere Angaben den aktuellen Kongruenzsatz Seite Winkel Seite.
Wir konstruieren im Folgenden das Dreieck. Wir beginnen mit der Seite a:
![]()
Anschließend zeichnen wir erst einmal den Winkel zwischen a und b ein:
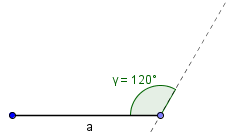
Und messen an der entstandenen Gerade die Strecke b = 2 cm ab.
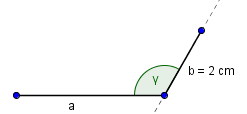
Als letztes müssen wir die beiden Punkt nur noch verbinden und erhalten so das fertig konstruierte Dreieck.
Kongruenzsatz: Winkel Seite Winkel
Bei diesem Kongruenzsatz haben wir von einem Dreieck nur eine Seite gegeben. Außerdem wissen wir die beiden Winkel die an die gegebene Seite grenzen. Dadurch ist das Dreieck eindeutig beschrieben. Wie wir es mit diesen Angaben konstruieren können zeigen wir anhand eines Beispiels.
Beispiel
Wir haben eine Seite und die beiden angrenzenden Winkel gegeben:

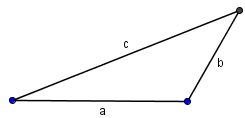
Wir beginnen mit der gegebenen Seite b:
![]()
Anschließend zeichnen wir die beiden gegebenen Winkel an den beiden Endpunkten ein:
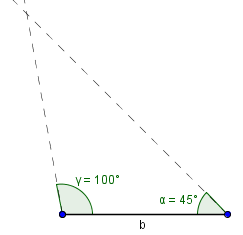
Den Schnittpunkt müssen wir nun nur noch markieren und die beiden verbleibenden Seiten einzeichnen:
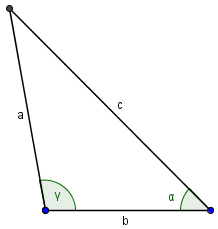
Natürlich hätten wir auch die beiden Winkle nach unten einzeichnen können. Wir hätten dann ein kongruentes Dreieck erhalten.
Kongruenzsatz: Seite Seite Winkel
Bei diesem Kongruenzsatz haben wir zwei Seiten und den Winkel, der der längeren Seite gegenüberliegt gegeben. Dadurch ist ein Dreieck eindeutig beschrieben.
Beispiel
Wir haben zwei Seiten und den Winkel, der der längeren Seite gegenüberliegt gegeben:
c = 6cm
b = 3cm
γ = 70°
Mithilfe dieser Angaben werden wir das gesuchte Dreieck konstruieren. Wir beginnen mit der kurzen Seite b.
![]()
Jetzt zeichnen wir den Winkel ein:
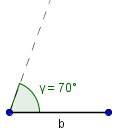
Jetzt zeichnen wir um den anderen Punkt einen Kreis mit einem Radius von 6 cm und markieren den Schnittpunkt mit der zuvor gezeichneten Geraden.
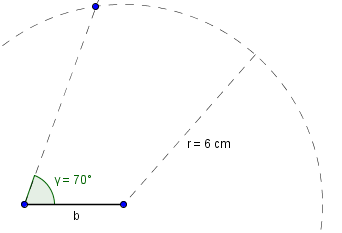
Abschließend müssen wir nur noch die drei Punkte verbinden und erhalten so das gesuchte Dreieck.