Flächeninhalt eines Parallelogramms
Ein Parallelogramm ist ein Rechteck bei dem die Winkel nicht 90° betragen müssen. Die gegenüberliegenden Seiten müssen parallel sein.
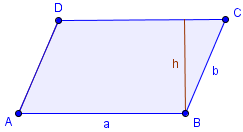
Der Flächeninhalt kann mit folgender Formel berechnet werden:
![]()
Unser Lernvideo zu : Flächeninhalt eines Parallelogramms
Die wichtigsten Eigenschaften des Parallelogramms
In jedem Parallelogramm stellen wir zwei Innenwinkel zu je 180° nebeneinander fest. Unser geometrisches Gebilde wird zu einem Rechteck, wenn die jeweils benachbarten Seiten zu einem rechten Winkel zusammenlaufen. Auch die Diagonalen müssen beim Rechteck gleichlang sein. Unser Parallelogramm wird zum Rhombus bei gleichlangen Seiten.
Ihr fragt euch, wie ihr ein Parallelogramm konstruieren könnt? Am Mittelpunkt einer Dreiecksseite spiegelt ihr das Dreieck einfach nochmal, schon ist das Parallelogramm fertig. Der Schnittpunkt bildet eine Diagonale, die mit M beschrieben wird.
Hier liefern wir euch nochmals die wichtigsten Eigenschaften vom Parallelogramm auf einen Blick:
∗ gegenüberliegende Seiten gleich lang
∗ gegenüberliegende Seiten schneiden sich nicht
∗ gleich große Winkel, die sich gegenüber liegen
∗ Diagonalen halbieren sich
∗ benachbarte Winkel zusammen auf 180°
∗ punktsymmetrisch
Gerade in der Mechanik treffen wir sehr oft auf das Parallelogramm, das eine bewegliche und parallele Lagerung ermöglicht.
Wie du den Flächeninhalt eines Parallelogramms berechnen kannst?
Die jeweilige Fläche bezeichnen wir mit dem großen Buchstaben F. Wir müssen das Parallelogramm in seine einzelnen Teile zerlegen, um auf die Gesamtfläche zu kommen. Dann könnt ihr auch die einzelnen Formen zum Flächeninhalt besser nachvollziehen.
Beispiel
a = 8 cm
b = 4 cm
h = 3 cm
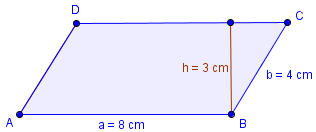
![]()
Der Flächeninhalt dieses Parallelogramms beträgt 24 cm². Die Angabe von der Seite b hätten wir für die Berechnung des Flächeninhalts nicht gebraucht. Allerdings ist b notwendig, damit das Parallelogramm eindeutig gezeichnet werden kann.
Herleitung
Wir bedienen uns für die Flächenberechnung wieder der Formel für das Rechteck und machen folgendes:
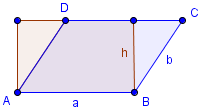
Wir zeichnen also ein Rechteck, welches dieselbe Grundseite und dieselbe Höhe hat, wie das Parallelogramm. Der Flächeninhalt des Rechtecks und des Parallelogramms ist derselbe, da die beiden eingefärbten Flächen der nächsten Grafik gleichgroß sind:
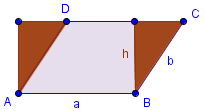
Wir machen für die Flächenberechnung aus dem Parallelogramm ein Rechteck indem wir rechts ein Stück wegnehmen und dieses links wieder an das Parallelogramm dransetzen.
Die Formel für den Flächeninhalt des Parallelogramms ist deshalb ähnlich wie die für das Rechteck:
![]()
Wir müssen also eine Grundseite mit der dazugehörigen Höhe multiplizieren.
Übungsaufgaben zum Parallelogramm
Berechne aus den folgenden Angaben den Umfang des Parallelogramms!
1. b = 9 cm a = 8 cm
2. b = 46 m a = 2900 cm
3. a = 6,3 m b = 3,9 m
Berechne ausgehend von der Höhe und der Seite den Flächeninhalt des Parallelogramms!
1. h = 18 cm a = 7 cm
2. a = 6 dm h = 5,4 m
3. b = 4,4 cm h = 9 cm
Die Lösungen zu den oben stehenden Übungsaufgaben
U = 2 • a + 2 • b
1. 34 cm | 2 • 9 + 2 • 8 = 18 + 16 = 34 cm
2. 150 m | 2 • 29 + 2 • 46 = 58 + 92 = 150 m
3. 20,4 m| 2 • 6,3 + 2 • 3,9 = 12,6 + 7,8 = 20,4 m
A = g • h
1. 126 cm | 18 • 7 = 126 cm
2. 324 m | 6 • 54 = 324 dm
3. 39,6 cm | 4,4 • 9 = 39,6 cm
