Urnenmodell
Was versteht man unter einer Urne
- Unter einer Urne versteht man ein beliebiges Gefäß, in dem sich n Elemente („Kugeln“) befinden, aus denen per Zufall k Elemente herausgezogen werden (d. h. ohne dass beim Ziehen in das Gefäß hineingesehen werden und bewusst ausgewählt werden kann).
- Urnenmodelle werden vor allem dazu verwendet, die Anzahl der Elemente für Ergebnismengen von Zufallsexperimenten zu bestimmen
- Man stellt sich dabei vor, man hat eine Urne mit N–unterscheidbarenKugeln und zieht aus dieser n-mal. Wichtig ist, dass alle Kugeln in der Urne die gleiche Wahrscheinlichkeit besitzen, gezogen zu werden
⇒Das Ziehen kann auf zwei verschiene Arten erfolgen
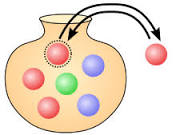
- Eine Kugel wird gezogen und wieder zurückgelegt. Das entspricht dem Urnenmodell mit Zurücklegen
- Nach dem ziehen der Kugel wird diese nicht wieder zurückgelegt. Das entspricht dem Urnenmodell ohne Zurücklegen
Kombinatorische Prinzipien
Man hat vier verschiedene Arten von Urnenmodellen. Zentrale Frage dabei ist immer, ob man die Kugeln nach dem Zug wieder zurücklegt (oder nicht) und ob man die Reihenfolge der Ziehung beachtet (oder nicht).
Die Formeln zur Berechnung der Möglichkeiten sehen wie folgt aus:

Unser Lernvideo zu : Urnenmodell
Beispiel 1
Ein Würfel wird fünfmal geworfen. Wie viele Wurfergebnisse kann es geben?
Ein Wurfergebnis ist ein 5-Tupel, dessen Stellen mit den Ziffern 1 bis 6 besetzt werden.
Hier ist eine Anordnung der einzelnen Wurfergebnisse gegeben (erster Wurf, zweiter Wurf, …). Bei jedem Wurf kann eine Augenzahl zwischen 1 und 6 auftreten. Es liegt also eine 5-Variation mit Wiederholung aus der Menge {1, 2, 3, 4, 5, 6} vor. Es ist n = 6 und k = 5, also gibt es
![]()
verschieden Wurfergebnisse.
Beispiel 2
Von den 16 Mannschaften, die am UEFA-Cup eines bestimmten Jahrganges teilnehmen, seien 2 Mannschaften aus Deutschland. Wie groß ist die Wahrscheinlichkeit, dass die beiden deutschen Mannschaften in der ersten Runde gegeneinander spielen? (mit Reihenfolge und ohne Zurücklegen)
Lösung
![]()
