Tupel
Tupel bzw. Aufzählprinzip
- Das Zählprinzip sagt etwas über die Anzahl der Möglichkeiten aus, wie ein Zufallsexperiment ausgehen kann.
- Man definiert ein Tupel der Länge n als eine Aufzählung von n nicht notwendig von einander verschiedenen mathematischen Objekten in einer vorgegebenen, festen Reihenfolge.
- Stellt man n Elemente einer Menge in einer bestimmten Reihenfolge zusammen und lässt man dabei auch Wiederholungen zu, so entsteht eine Folge der Länge k.
Unterschied zwischen n-Tupel und k-Tupel
- Ein n-Tupel ist das Ergebnis eines n-Stufigen Zufallsexperiments
Du führst n-Mal das selbe Zufallsexperiment durch und notierst Dir in der Reihenfolge die Ergebnisse. Das ergibt dann Deine n-Tupel: n-Mal ein Ergebnis eines Zufallsexperiments. Da ist nichts darüber ausgesagt, was die Grundmenge der Ergebnisse ist! Demzufolge auch nicht, wie viele verschiedene Ergebnisse es überhaupt gibt.
- Die Anzahl an k-Tupeln ist definiert als n^k ,also einem Tupel mit k-Werten aus einer n-Menge
Hier wird kein k-Tupel definiert!!! Hier wird nur die Anzahl von k-Tupeln unter einer ganz speziellen Voraussetzung definiert! Was hier beschrieben wird ist ein k-stufiges Zufallsexperiment! Aber anders als bei der Definition des n-Tupel wird hier eine endliche Grundmenge mit genau n Elementen, n verschiedenen Elementen, vorausgesetzt. Das Zufallsexperiment ist die Auswahl von k Elementen aus der n-elementigen Grundmenge, wobei es auf die Reihenfolge der Auswahl genauso ankommt, wie es möglich ist, daß ein und das selbe Element noch einmal ausgewählt wird. Es geht um eine Auswahl von k Elementen aus einer n-elementigen Grundmenge unter Beachtung der Reihenfolge und mit Wiederholung (auch mit Zurücklegen genannt).
Zählprinzip für Mengen.
- Dafür benötigt man den so genannten Binomialkoeffizient. Dieser gibt an, auf wie viele verschiedene Arten man k Objekte aus einer Menge von n verschiedenen Objekten auswählen kann. Der Versuch wird dabei ohne Zurücklegen und ohne Beachtung der Reihenfolge durchgeführt. Man könnte auch sagen: Die Anzahl der Möglichkeiten in einem n-Tupel genau k Plätze zu reservieren. Für das Zählprinzip bzw. die Berechnung des Binomialkoeffizienten gilt folgende Formel.
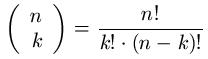
Unser Lernvideo zu : Tupel
Beispiel
In einer Urne befinden sich 30 Kugeln, die von 1 bis 30 durchnummiert sind. Aus der Urne sollen 6 Kugeln gezogen werden. Die gezogenen Kugeln werden nicht zurückgelegt und die Reihenfolge der Kugeln ist nicht von Interesse. Wie viele Möglichkeiten gibt es, diese Kugeln zu ziehen?
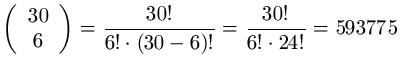
Beispiel
Markus besitzt 3 Paar Schuhe, 2 Hosen und 4 T-Shirts. Wie oft muss er sich anziehen, wenn er alle Kombinationsmöglichkeiten ausprobieren will?
Lösung
Zu jedem seiner 3 Paar Schuhe hat er 2 Möglichkeiten, eine Hose hinzuzufügen.
Damit gibt es 3⋅2=6 Schuhe-Hose-Kombinationen.
Zu jeder dieser 6 Möglichkeiten hat er 4 verschiedene T-Shirts zur Auswahl:
Damit gibt es insgesamt 3⋅2⋅4=24 Schuhe-Hose-T-Shirt-Kombinationen
Merke Dir
- Die Anzahl der Komponenten eines Tupels nennt man die Arität des Tupels. Das Tupel (7,8,9) hat also beispielsweise die Arität 3.
- Für bestimmte n-Tupel gibt es spezielle Namen:
- Ein 2-Tupel nennt man beispielsweise auch Paar,
- Ein 3-Tupel nennt man auch Tripel,
- Ein 4-Tupel nennt man auch Quadrupel,
- Ein 5-Tupel nennt man auch Quintupel, und
- Ein 8-Tupel nennt man auch ein Oktupel.
- Ein 1-Tupel wird manchmal auch als Singel bezeichnet.
