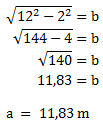Satz des Pythagoras
Der Satz des Pythagoras hilft uns Seitenlängen in rechtwinkligen Dreiecken zu berechnen. Er lautet folgendermaßen:
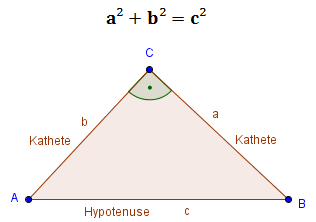
a und b werden als Katheten bezeichnet, c ist die Hypotenuse. Die Hypotenuse ist die längste Seite und liegt immer dem rechten Winkel gegenüber. Die beiden kürzeren Seiten sind die Katheten a und b.
Der Satz des Pythagoras sagt also, dass wir das Quadrat der Hypotenuse erhalten, wenn wir die Quadrate der beiden Katheten addieren. Sobald wir also zwei Seiten im rechtwinkligen Dreieck kennen, können wir die dritte berechnen.
Lerntool zu Satz des Pythagoras
Unser Lernvideo zu : Satz des Pythagoras
Den Satz des Pythagoras endlich verstehen
Wir haben es beim Satz des Pythagoras mit einem der grundlegenden Lehrsätze in der Geometrie zu tun, ohne den ihr keinen Schritt weiter kommt. Mittlerweile finden sich unzählige Beweise für diesen Satz. Wobei es immer noch vielen Schülern Probleme bereitet, den Inhalt wirklich zu verstehen.
Tatsächlich gibt es ganze Bücher, die sich einzig und allein mit dem Beweisen der Erklärung dieser Regel befassen. Eine der wichtigsten Formen, die für einen Beweis sorgen, sind Quadrate, die zum einen an der Fläche der Hypothekengröße und an den zwei rechtwinkligen Seiten liegen. So passt der Inhalt der beiden kleineren Quadrate in das größere Quadrat perfekt hinein. Daraus ergibt sich die These.
Satz des Pythagoras: In einem rechtwinkligen Dreieck ist die Summe der Kathetern gleich dem Quadrat der Hypotenuse.
Grundsätzlich kommt ihr zum ersten Mal in der 8. und in der 9. Klasse in Berührung mit diesem Satz und der dazugehörigen Rechenformel. Neulingen ist zu raten, sich von Anfang an tiefgründig damit auseinander zusetzen. Denn dieser Satz des Pythagoras taucht immer wieder in anderen Mathematikbereichen auf.
Im Prinzip sagt er nichts weiter, als dass das die Summe der Flächeninhalte der Quadrate der Kathetern gleich der Summe der Quadrate der Hypothyreose ist. Um das Ganze zu vereinfachen, gibt man den Seiten einfach Bezeichnungen mit kleineren Buchstaben, wie A, B und C.
- a und b liegen jeweils an dem rechten Winkel und werden als Kathetern bezeichnet.
- c liegt im rechten Winkel gegenüber.
Wer hat den Satz des Pythagoras bewiesen?
Zuerst war es Samos, der einen mathematischen Beweis gefunden hat. Wobei wir uns hier nicht festlegen wollen, da die historische Begründung oftmals umstritten ist. Aus der Umkehrung des Satzes kann man ganz einfach überprüfen, ob ein Dreieck auch rechtwinklig ist. Dabei testet ihr, ob die Gleichung für die Seiten des Dreiecks zutrifft.
Ihr braucht nichts weiter als die Seiten eines Dreiecks zu kennen, um herauszufinden ob es rechtwinklig ist. Wie praktisch ein einziger Satz doch sein kann, oder?
Die korrekte Verwendung des Satz des Pythagoras
Haben wir es also mit einem Dreieck mit den Seitenlängen 3,4 und 5 cm zu tun, ist es tatsächlich rechtwinklig.
Darüber hinaus ergibt sich aus diesem Satz auch die Tatsache, dass rechtwinklige Dreiecke eine Hypotenuse haben, die eigentlich länger ist – als die beiden Katheten. Das brauchen wir in der Dreiecksungleichung.
Beispiel 1
a = 5 cm
b = 3 cm
c = ?
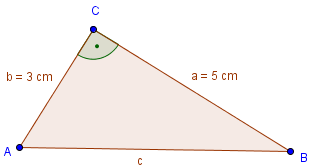
Wir müssen die fehlende Seite c berechnen. Hierfür benutzen wir den Pythagoras. Damit wir c berechnen können, müssen wir die Wurzel ziehen:
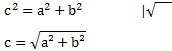
Jetzt können wir die Werte einsetzen und c berechnen. Die Einheit ist cm. Wir lassen diese bei der Rechnung weg, wissen aber, dass das Ergebnis die Einheit cm hat. Wichtig ist immer, dass die eingesetzten Größen dieselbe Einheit haben. Wenn sie unterschiedliche Einheiten hätten, müssten wir sie zunächst umrechnen.
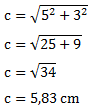
Die Seite c ist 5,83 cm lang.
Beispiel 2
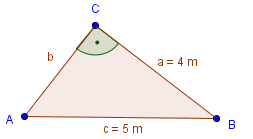
a = 4 m
b = ?
c = 5 m
Wir zeichnen zunächst einmal das Dreieck, damit man sich das Problem besser vorstellen kann. Man kann die fehlende Größe aber auch berechnen ohne das Dreieck zu zeichnen.
Wir müssen nun eine fehlende Kathete b berechnen. Hierfür ist es notwendig die Formel nach b umzustellen. Wir sorgen durch eine Umformung dafür, dass b alleine steht:
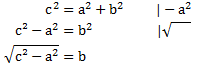
Jetzt setzen wir die Werte ein:
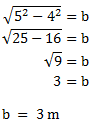
Damit haben wir die fehlende Seite berechnet und die Aufgabe gelöst.
Beispiel 3
a = ?
b = 2 m
c = 12 m
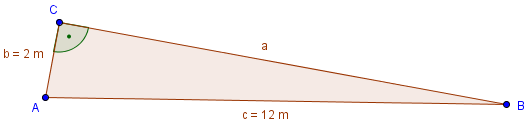
In diesem Fall müssen wir den Satz des Pythagoras nach a umformen:
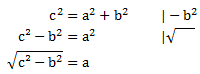
Und anschließend die Werte einsetzen: