Kathetensatz
Wir kennen den Satz des Pythagoras nun und wollen uns als nächstes mit der erweiterten Anwendung dieses Satzes befassen. Zum einen ist das der Kathetensatz des Euklids.
Euklid war ein griechischer Mathematiker, der zum einen das damalige Wissen der mathematik zusammengefasst und einheitlich dargestellt hat und besonders auf eine strenge Beweisführung geachtet hat. Dieses ist noch heute Grundlage und Vorbild in der Mathematik. Zusätzlich hat er auch neue Erkenntnisse, Axiome und Beweise durchgeführt.
Definition
Die Verlängerung der Höhe eines rechtwinkligen Dreiecks teilt das Hypothenusenquadrat in zwei Rechtecke. Je eines der Rechtecke hat die selbe Fläche wie das Quadrat über eines der Katheten.
Unser Lernvideo zu : Kathetensatz
Erklärung
Um den Kathetensatz besser zu verstehen, hilft am ehesten eine Zeichnung.
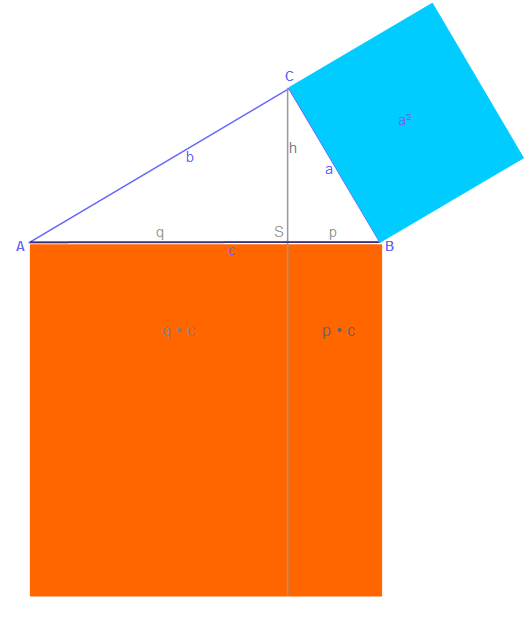
In der Abbildung seht ihr ein blaues Dreieck ABC. Dieses ist in C rechtwinklig. Die Hypothenuse ist c und das Hypothenusenquadrat c² ist hier orange eingezeichnet.
Zeichnen wir nun die Höhe des Dreiecks ein, läuft die Höhe durch den Punkt C senkrecht zur Seite c und schneidet die Seite im Punkt S uns teilt sie in zwei Abschnitte q und p. Nun ist die Strecke q von A bis S und die Strecke p von S bis B.
Wenn wir nun die Höhenlinie weiter zeichnen teilen wir das Hypothenusenquadrat in zwei Rechtecke. Das eine hat die Maße q • c und das andere ist p • c.
Der Kathetensatz besagt nun, dass jedes der Rechtecke den selben Flächeninhalt hat wie je eines der beiden Kathetenquadrate. So meint es, dass das Rechteck p • c = a² ist.
Dies gilt auch für das andere Kathetenquadrat über der Kathete b. Dies wäre: q • c =b².
Formeln
a² = p • c
b² = q • c
Beweis
Um den Kathetensatz beweisen zu können, schauen wir uns die Gegebenheiten an. In unserer Abbildung haben wir drei rechtwinklige Dreiecke. ABC, BCS ( 90° in Punkt S) und CAS (90° in Punkt S).
1. a² + b² = c²
2. q + p = c
3. (q + p)² = c²
4. h² + p² = a² (Abwandlung des Satzes des Pythagoras)
5. h² + q² = b² (Abwandlung des Satzes des Pythagoras)
Nun können wir einsetzen. Wir wollen beweisen, dass es gilt a² = p • c
Als erstes ersetzen wir c²:
a² + b² = (q + p)²
Dann ersetzen wir a² und b²:
h² + p² + h² + q² = (q + p)²
Nun fassen wir zusammen und lösen die binomische Formel auf
2h² + p² + q² = q² +2qp + p²
Es wird auf beiden Seiten q² und p² abgezogen
2h² = 2qp
Wir teilen durch 2
h² = qp
Nun kommt der zweite Schritt in dem wir das Ergebnis in unsere 4. Formel von oben setzen: a² = h² + p²
a² = h² + p²
Ersetzen von h²
a² = qp + p²
Ausklammern von p
a² = p (q + p)
Wir wissen q + p = c und setzen dieses ein
a² = p • c
Somit haben wir bewiesen, dass der Kathetensatz gilt. Das selbe Verfahren wendet man an, um zu beweisen, dass b² = q • c.
