Anwendung des Höhensatzes
Nachdem wir erklärt haben, was der Höhensatz ist und wie wir ihn beweisen können, interessieren wir uns nun für seine Anwendung. Dazu schauen wir uns einige Beispiele an.
Zur Erinnerung
Die Formel des Höhensatzes lautet:
h² = q • p
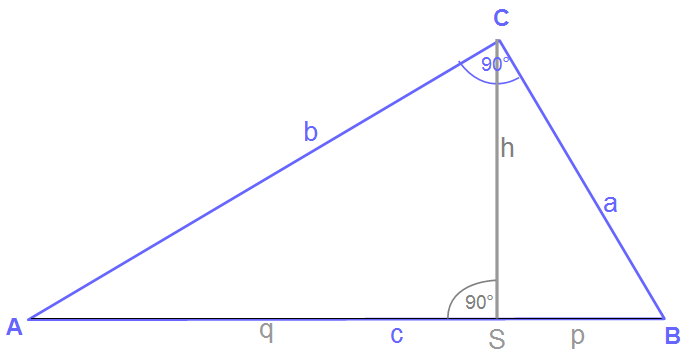
Zur Erinnerung ist nochmal die Formel und ein rechtwinkliges Dreieck dargestellt. So kann man sich nochmal vergegenwärtigen, wie sich der Höhensatz zusammensetzt.
Lerntool zu Anwendung des Höhensatzes
Übung 1
In einem rechtwinkligem Dreieck sind die beiden Hypothenusenabschnitte gegeben. Wie lang ist die Höhe des Dreiecks?
p = 18 mm
q = 25 mm
gesucht ist h
1. Schritt: Notieren der Formel
h² = q • p
2. Schritt: Einsetzen in die Formel und berechnen
h² = 25mm • 18mm
h² = 450 mm² | Wurzel ziehen
h = 21,21 mm
Somit haben wir mit dem Höhensatz die Höhe h errechnen können.
Übung 2
In einem rechtwinkligem Dreieck ist die Höhe und ein Hypothenusenabschnitt gegeben. Wie lang ist der noch fehlende Hypothenusenabschnitt?
h = 15 cm
p = 20 cm
gesucht ist q
1. Schritt: Formel notieren und umstellen nach der gesuchten Variablen
h² = q • p | :p
h²/p = q
q = h²/p
2. Schritt. Einsetzen in die Formel und berechnen
q = (15cm)²/20cm
q = 225cm²/20cm
q = 11,25 cm
Wir konnten durch umstellen der Formel zum Höhensatz unseren unbekannten Hypothenusenabschnitt berechnen.
