Schnittpunkt von zwei quadratischen Funktionen
Wenn wir den Schnittpunkt von zwei quadratischen Funktionen bestimmen möchten, müssen wir die beiden Funktionen einfach gleichsetzen und die Gleichung anschließend nach x auflösen. Wir erhalten keinen, einen oder zwei x-Werte für den Schnittpunkt. Indem wir die x-Werte in eine der Funktionen einsetzen, erhalten wir den y-Wert des jeweiligen Schnittpunkts.
f(x) = g(x)
Unser Lernvideo zu : Schnittpunkt von zwei quadratischen Funktionen
Beispiel
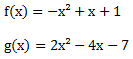
Wir setzen die beiden Funktionen gleich und Formen diese nach x um, indem wir zunächst alles auf die linke Seite bringen.
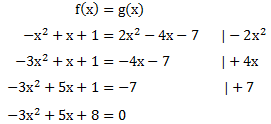
Diese Gleichung lösen wir nun genauso wie wir es auch bei der Berechnung der Nullstellen gemacht haben. Wir benutzen dafür in diesem Beispiel die PQ-Formel. Alternativ könnte man natürlich auch den Weg über die quadratische Ergänzung gehen.
Zunächst müssen wir die Gleichung normalisieren:
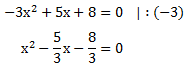
Als Parameter für die PQ-Formel erhalten wir:
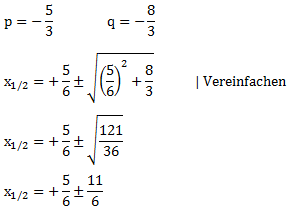
Wir machen eine Fallunterscheidung:
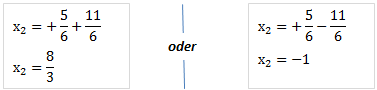
Damit haben wir die beiden x-Werte der Schnittpunkte. Um die y-Werte zu erhalten, müssen wir die beiden Werte in eine der beiden Funktionen einsetzen. Wir setzen sie zur Kontrolle in beide ein und überprüfen ob wir bei beiden den gleichen y-Wert erhalten.
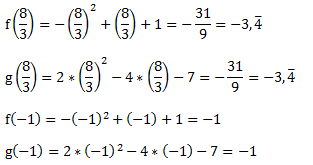
Die Schnittpunkte sind also:
![]()
Hier noch einmal die gezeichneten Funktionen:
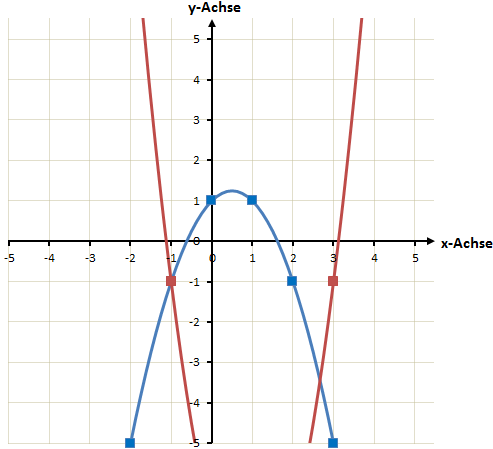
Natürlich hätten wir die Schnittpunkte auch grafisch ablesen können. Dies wäre allerdings nicht so genau wie die rechnerische Lösung.
Beispiel: Ein Schnittpunkt
Wir möchten hier noch ein Beispiel vorstellen bei dem die beiden Funktionen genau einen Schnittpunkt haben.
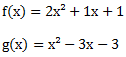
Wir gehen genauso wie bei dem vorherigen Beispiel vor.
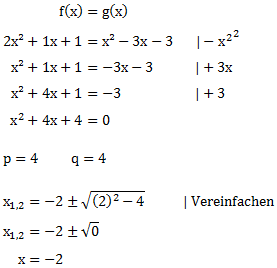
Es gibt also nur genau einen Schnittpunkt der bei x=-2 liegt. Um den y-Wert zu bestimmen setzen wir den Wert in die Funktionen ein:
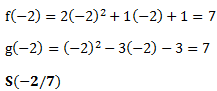
Wir gucken uns dies noch einmal an den gezeichneten Funktionen an und überprüfen das Ergebnis.
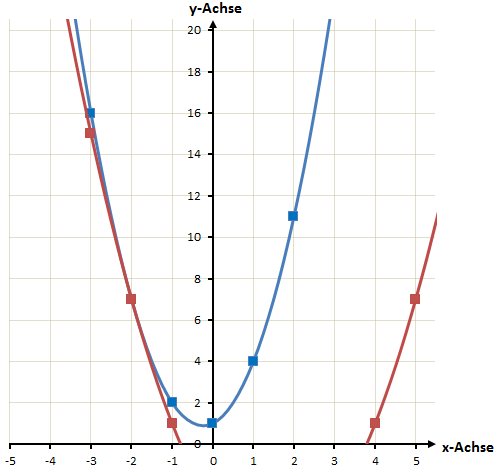
Auch bei diesem Beispiel hätten wir den Schnittpunkt vermutlich nur sehr ungenau ablesen können. Es ist deshalb wichtig den rechnerischen Weg zu kennen.
