Definitionsbereich bestimmen bei Funktionen
1)Wie ist der Definitionsbereich definiert?
Der Definitionsbereich ist definiert als die Menge aller Werte die, eingesetzt in die Funktion, einen Wert liefern. Mit anderen Worten ist der Definitionsbereich die gesamte Menge an x-Werten, die in eine Funktion eingesetzt werden können, und einen y-Wert liefern.
2) Wie finde ich den Definitionsbereich für eine Auswahl an Funktionen?
Der Funktionstyp bestimmt die beste Methode um den Definitionsbereich zu bestimmen.
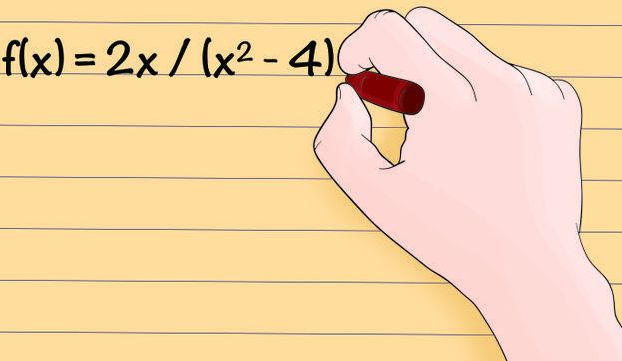
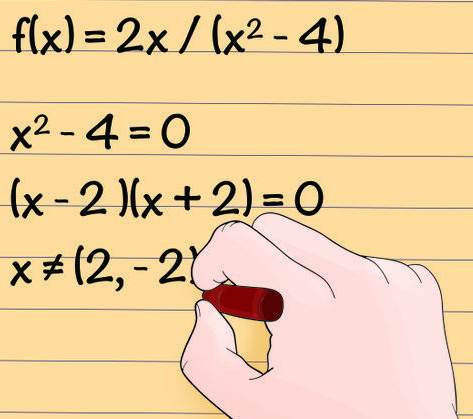
Bei Brüchen mit einer Variablen im Nenner setze den Nenner gleich 0. Beim Bestimmen des Definitionsbereiches einer Funktion mit Brüchen musst du alle x-Werte, die den Nenner zu 0 machen, ausschließen, denn die Division durch 0 ist nicht erlaubt. Schreibe den Nenner also als Gleichung und setze sie gleich 0. Hier siehst du wie es geht:
- Eine Polynom-Funktion ohne Wurzeln und Variablen im Nenner. Bei diesem Funktionstyp ist der Definitionsbereich alle reellen Zahlen.
- Eine Funktion mit einem Bruch mit einer Variablen im Nenner. Um den Definitionsbereich für diesen Funktionstyp zu finden setze den Nenner gleich 0 und schließe den Wert aus, den du erhältst, wenn du nach der Variablen auflöst.
- Eine Funktion mit einer Variablen unter der Wurzel. Um den Definitionsbereich für diesen Funktionstyp zu finden setze den Ausdruck unter der Wurzel > 0 und löse nach der Variablen auf, so dass du die Werte findest, die du einsetzen darfst.
- Eine Funktion mit dem natürlichen Logarithmus (ln). Um den Definitionsbereich für diesen Funktionstyp zu finden setze das Argument des Logarithmus > 0 und löse nach der Variablen auf.
- Ein Graph. Überprüfe den Graphen um zu sehen welche Werte du für die Variable einsetzen darfst.
- Eine Relation. Das ist eine Liste mit x- und y-Koordinaten. Dein Definitionsbereich ist dann einfach eine Liste mit x-Koordinaten.
3) Schreibe den Definitionsbereich richtig auf.
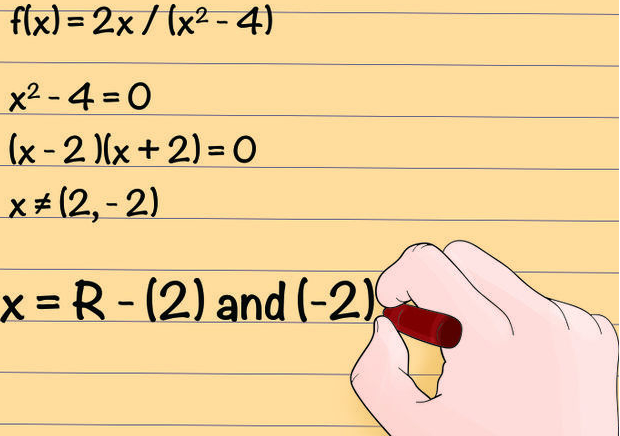
f(x) = 2x/(x2– 4)
x2- 4 = 0
(x – 2 )(x + 2) = 0
x ≠ (2, – 2) ► x = alle reellen Zahlen außer 2 und -2 Hier sind ein paar Dinge, die man wissen sollte über das Aufschreiben eines Definitionsbereich:
- Das Format für den Definitionsbereich ist eine linke Klammer, dann Anfangs- und Endpunkt des Definitionsbereiches getrennt durch ein Komma und dann eine rechte Klammer.
- Zum Beispiel [-1,5). Das bedeutet der Definitionsbereich geht von -1 bis 5.
- Benutze eckige Klammern, [ und ], falls die Zahl zum Definitionsbereich gehört.
- Im Beispiel [-1,5) ist -1 im Definitionsbereich enthalten.
- Benutze runde Klammern, ( und ), falls die Zahl nicht zum Definitionsbereich gehört.
- Im Beispiel [-1,5) gehört 5 nicht zum Definitionsbereich. Der Definitionsbereich geht beliebig nahe an 5 heran, d.h. 4.999…
- Benutze “U” (das heißt „Vereinigung“) um Teile des Definitionsbereiches, die durch Lücken getrennt sind, zu verbinden.‘
- Zum Beispiel [-1,5) U (5,10]. Das heißt dass der Definitionsbereich von -1 bis 10 inklusive geht, aber dass es eine Definitionslücke bei 5 gibt. Das kann vorkommen wenn eine Funktion zum Beispiel “x – 5” im Nenner stehen hat.
- Du kannst so viele „U“-Symbole wie nötig verwenden, wenn der Definitionsbereich mehrere Lücken hat.
- Benutze das „Unendlich“-Zeichen (mit + oder -) um auszudrücken, dass der Definitionsbereich in dieser Richtung unendlich weiter geht.
- Benutze immer ( ) und nicht [ ], wenn du das Unendlich-Symbol verwendest.
Weitere Beispiele
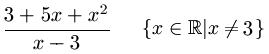
denn,
- Es darf nicht durch Null dividiert werden
- Aus einer negativen Zahl darf keine Wurzel gezogen werden
Definitionslücken
Um den Definitionsbereich einer Funktion zu bestimmen, muss man sie auf Definitionslücken prüfen.
Definitionslücken sind Werte, die in eine Funktion nicht eingesetzt werden dürfen. Man muss also prüfen, ob durch einen bestimmten x-Wert
- der Nenner eines Bruches 0 würde
- etwas Negatives unter einer Wurzel stünde
- das Argument eines Logarithmus kleiner oder gleich 0 wäre.
Definitionsränder
- Soll das Verhalten an den Definitionsrändern untersucht werden, so muss man das Verhalten des Graphen links und rechts der Defitiontionslücken betrachten, sowie meistens das Verhalten des Graphen im Unendlichen. Dies funktioniert mit Hilfe der Grenzwertbetrachtung
