Wurzelrechnung – Einführung
Im Folgenden werden wir die unterschiedlichen Fragen und Begriffe des Themas Wurzelrechnung bearbeiten.
Was sind Wurzeln?
Mit einer Wurzel bezeichnet man die Wurzelrechnung. Dies ist die Umkehrfunktion einer Potenzierung.
Wir wissen: an = b
dabei kennen wir die Basis a und den Exponenten n und konnten b berechnen.
Bei einer Wurzelrechnung wollen wir nun den Wurzelwert a herausfinden, wenn der Wurzelexponent n und der Radikant b bekannt sind. Daher fragen wir uns: Welche Zahl a muss ich mit n potenzieren um b zu erhalten.
Definition:
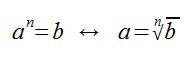
Wir sprechen: a hoch n gleich b – ist äquivalent zu – a ist gleich n-te Wurzel aus b
Beispiel 1:
![]()
Beispiel 2:
![]()
Was sind Quadratwurzeln?
Unter der Quadratwurzel verstehen wir die „klassische“ Wurzel, sie wird auch „zweite Wurzel“ genannt. Wenn eine Quadrierung, also eine Rechnung mit „hoch 2“, zurückgerechnet werden soll, nutzen wir den Wurzelexponenten 2.
Beispiele:
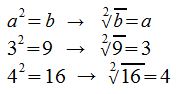
Wenn kein Wurzelexponent angegeben wird, ist direkt die Quadratwurzel gemeint!
Beispiele:
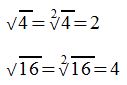
Man spricht: 1) Die Wurzel aus 4 ist gleich 2.
2) Die Quadratwurzel aus 4 ist gleich 2
3) Die zweite Wurzel aus 4 ist gleich 2.
Alle drei Aussagen bedeuten dasselbe!
Was ist eine Kubikwurzel?
Die Kubikwurzel wird auch dritte Wurzel genannt und enspricht dem Wurzelexponenten 3. Sie ist die Umkehrung der Berechnung mit „Hoch 3“.
Beispiele:
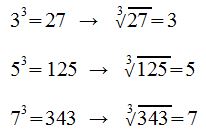
Man spricht: 1) Die Kubikwurzel aus 27 ist gleich 3.
2) Die dritte Wurzel aus 125 ist gleich 5.
Beide Aussagen drücken dasselbe aus!
Gibt es noch andere Wurzeln?
Ganz klare Antwort: Ja!
Es gibt zu jedem Exponenten auch eine Wurzel. Dies drückt mal allgemein als n-te Wurzel aus. Hier ist das n ein Platzhalter für den gewollten Wurzelexponenten.
Beispiele:
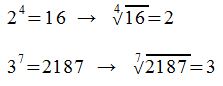
Man spricht: Die vierte Wurzel aus 16 ist gleich 2. Und die siebte Wurzel aus 2187 ist gleich 3.
Hier gibt es keine andere Ausdrucksweise.
Unser Lernvideo zu : Wurzelrechnung – Einführung
Wie schreibe ich Wurzeln als Potenz und warum?
Jede Wurzel kann auch als Potenz ausgedrückt werden. Dazu benötigt man einen gebrochenen Exponenten.
Allgemein gilt:
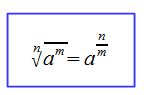
Beispiele:
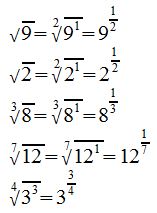
An den Beispielen sehen wir, dass es irrelevant ist, welcher Wurzelexponent oder welche Potenz unter der Wurzel steht. Die Umformung geschieht imme auf dem gleichen Weg.
Diese Umformung kann man nutzen, um sich Rechnungen zu vereinfachen, wenn man zum Beispiel leiber mit Potenzen als mit Wurzeln rechnet oder wenn sonst in der Rechnung nur Potenzen vorkommen.
Was sind gleichnamige und ungleichnamige Wurzeln?
Wurzeln sind gleichnamig, wenn der Wurzelexponent gleich ist.
Dementsprechend haben ungleichnamige Wurzeln verschiedenen Wurzelexponenten.
Beispiele für gleichnamige Wurzeln:
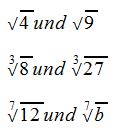
Die Wurzelexponenten sind gleich daher sind es gleichnamige Wurzeln. Der Radikant spielt dabei keine Rolle.
Beispiele für ungleichnamige Wurzeln:
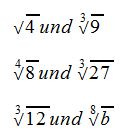
Die Wurzelexponenten sind unterschiedlich. Z.B. beim ersten Beispiel 2 und 3. Daher sind diese Wurzeln ungleichnamig. Auch hier ist der Radikant irrelevant.
Interessante Fragen und Antworten zu Wurzelrechnung – Einführung
Wie löse ich eine Wurzel? |
| Die GrundlagenDas Auflösen einer Wurzel wird auch als Wurzelziehen bezeichnet. Hierbei gibt es ein paar Grundlagen, um eine Wurzel lösen zu können. Wichtig ist, dass das Rechnen mit Potenzen bekannt ist. Wenn beispielsweise gefragt ist, welches Ergebnis 6² hat, dann muss klar sein, dass hier 6 x 6 zum Ergebnis führt und 36 ist. Wenn aber nun a² = 49 gefragt ist, so lässt sich die Gleichung nur lösen, indem die Wurzel gezogen wird. a² = 49 (Auftrag: Wurzel ziehen): a = Wurzel(49). Wer die Wurzel ziehen möchte, muss sich fragen welche Zahlen für a eingesetzt werden müssen, sodass: a x a = 49 ergibt. Da 7 x 7 = 49 ist, ist die Wurzel aus 49 = 7.
Weitere Beispiele: a² = 16 I Wurzel a² = 121 I Wurzel Es gibt auch Wurzeln, welche in der Schule nur mithilfe des Taschenrechners gelöst werden können, wie etwa ?Wurzel 30. ACHTUNG: Es darf keine Wurzel aus negativen Zahlen gezogen werden! Das heißt, dass Wurzel -25 nicht aufgelöst werden kann. |
