Negative Wurzel
Wir wollen zuerst klären, was eigentlich die Wurzel ist
Eine Wurzel √ macht das Potenzieren rückgängig. Ziehen wir die Wurzel aus dem Potenzwert, so erhalten wir die ursprüngliche Basis. Was das meint, zeigt uns folgendes Beispiel:
32=9, denn (rückgängig gemacht) 2√ 9= 3
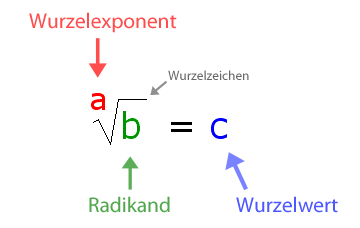
Es gibt drei wichtige Begriffe an der Wurzel, die ihr kennen müsst: Basis, Wurzelexponent und Wurzelwert
Wurzeln aus negativen Zahlen
- Allgemein ergeben sich für ungerade Potenzen negativer Zahlen wieder negative Zahlen.
- Man kann die Wurzel aus einer negativen Zahl ziehen. Nur nicht im Bereich der Menge IR.
- Im Bereich IR gibt es keine Zahl die mit sich selbst multipliziert eine negative Zahl ergibt. Daher kann ich im Bereich IR auch nicht die Wurzel aus einer negativen Zahl ziehen.
- Im Bereich der imaginären Zahlen ist dies allerdings möglich, weil dort die Wurzel aus -1 mit 1i definiert ist
Hierbei wird die imaginäre Einheit als i := √-1 definiert.
(Auch diese Schreibweise ist wieder nicht vollkommen korrekt, da ja mit i natürlich auch –i eine Wurzel aus -1 sein muss. Es ist daher besser zu sagen, wir definieren i durch die Eigenschaft: i² = -1.)
Nun wollen wir uns einen Beispiel anschauen,
X=√-1
Die Gleichung ist in R nicht lösbar, d.h. es gibt keine reelle Zahl R,
die eine Lösung dieser Gleichung ist. Dies erkennt man, wenn man
beide Seite der Gleichung quadriert. Man erhält:
X2 =-1
Nun sieht man: Die Gleichung hat keine Lösung in R, denn gleichgültig
welche reelle Zahl ich für x einsetzt: Die linke Seite wird nie negativ,
und somit auch nicht gleich –1.
Jetzt führen wir die Imaginäre Einheit i ein
- Wir haben gerade gezeigt, dass die Quadratwurzel aus –1 keine Lösung haben kann
√-1 = nicht definiert!
- Der Mathematiker Leonhard Euler (1707-1783) löste dieses Problem nun,indem er einfach eine neue Zahl „erfand“, welche die Lösung dieser Gleichung sein sollte, also die Wurzel aus –1. Er nannte diese Zahl i die „imaginäre Einheit“
√-1=i
- Quadriert man beide Seiten und vertauscht die Seiten der Gleichung, so erhält man die andere wichtige Schreibweise
i2= -1
Die imaginäre Einheit i kann man also auch als eine Zahl betrachten,
deren Quadrat die negative Zahl –1 ergibt.
Anwendung: Quadratwurzel aus negativen Zahlen
Nach der Einführung der imaginären Einheit i ist es uns möglich, auch aus
negativen Zahlen eine Quadratwurzel zu ziehen. Beispiel:
