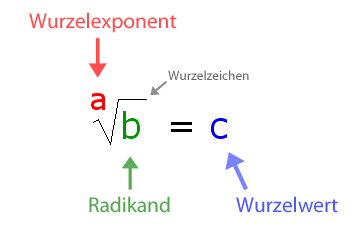
Definitionsbereich bei Wurzeln
- Wurzeln geraden Grades (also 2. Wurzel, 4. Wurzel …) sind nur definiert, wenn der Radikand (Term unter der Wurzel) größer oder gleich null ist. Bei diesen Funktionen müssen also diejenigen Bereiche ausgeschlossen werden, in denen der Radikand negativ wird.
Warum muss man bei Wurzelgleichungen die Definitionsmenge angeben?
- Der Radikant einer Wurzel darf niemals negativ werden. In solch einem Fall ist eine Wurzel nicht definiert und die zugehörige Gleichung nicht definiert.
Achte darauf
- Multipliziert man eine Ungleichung mit einer negativen Zahl (dividiert man durch eine negative Zahl), so wechselt das Ungleichzeichen seine Richtung.
- Multipliziere oder dividiere möglicht nicht mit einem Ausdruck, der eine Variable enthält. In solch einem Fall muss man verschiedene Fallunterscheidungen machen:
- der Ausdruck ist positiv – negativ (-> Richtungswechsel des Ungleich-Zeichens)
- der Ausdruck ist null (-> Umformung nicht erlaubt -> untersuche den Fall durch Einsetzten der entsprechenden Zahl. Überprüfe ob in diesem Fall die Gleichung erfüllt ist.
Unser Lernvideo zu : Definitionsbereich bei Wurzeln
Schreibweise
In den meisten Fällen besteht die Definitionsmenge aus allen reellen Zahlen, die größer gleich (bzw. kleiner gleich) einer reellen Zahl sind.
Beispiel
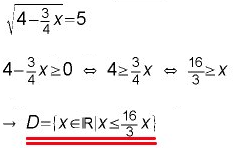
Beispiel 2
f(x) = √ x2-9
Der Radikand der Wurzel muss größer oder gleich null sein:
⇒x2 – 9 ≥ 0
⇒(x – 3)(x + 3) ≥ 0
Ein Produkt ist dann größer gleich null, wenn entweder beide Faktoren größer gleich null sind oder beide Faktoren kleiner gleich null sind:
►Fall 1: x – 3 ≥ 0 und x + 3 ≥ 0 ⇒ x ≥ 3 und x ≥ –3 ⇒ x ≥ 3 (dann ist zugleich x ≥ –3)
►Fall 2: x – 3 ≤ 0 und x + 3 ≤ 0 ⇒ x ≤ 3 und x ≤ –3 ⇒ x ≤ –3 (dann ist zugleich x ≤ 3)
Definitionsbereich: ID = {x | x ≤ –3 ∨ x ≥ 3}

Merke
Wie bestimmt man den Definitionsbereich einer Wurzelfunktion?
►Der Radikand( Term unter Wurzel) muss größer oder gleich Null sein!
►Ungleichung auflösen! ( falls du eine hast)
►efinitionsbereich aufschreiben: D={x<-R|Ungleichung}
