Kreiswinkelsatz
Der Kreiswinkelsatz wird auch Zentriwinkelsatz oder Mittelpunktswinkelsatz genannt. Diese drei Begriffe bezeichnen jeweils dasselbe und werden als Synonyme verwendet, um nicht zu oft einen Begriff zu verwenden! Auch wir werden zwischen den Begriffen wechseln, um euch nicht auf einen zu prägen und ihr genau wisst, wenn einer dieser Vokabeln fällt, worum es sich handelt.
Der Zentriwinkelsatz ist die Berechnung des Zentriwinkels. Der Zentriwinkel ist der Winkel am Mittelpunkt in einem Dreieck ABM, wobei die Punkte A und B auf dem Kreis liegen.
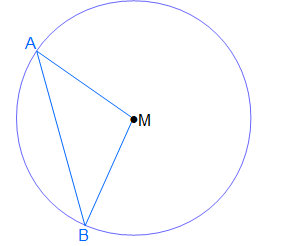
Die Aussage des Kreiswinkelsatzes ist: Der Mittelpunktswinkel ist doppelt so groß wie die Randwinkel.
Diese Aussage werden wir als nächstes prüfen und beweisen.
Unser Lernvideo zu : Kreiswinkelsatz
Erklärung
Die Aussage des Kreiswinkelsatzes: „Der Mittelpunktswinkel ist doppelt so groß wie die Randwinkel“ werden wir nun prüfen. Dazu nehmen wir uns ein allgemeines Beispiel als Vorlage.
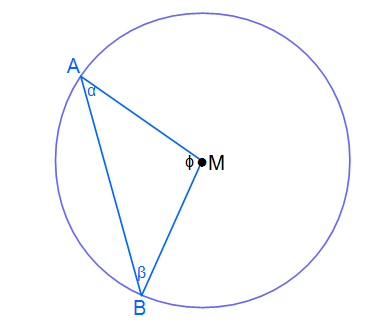
In der Abbildung seht ihr einen Kreis mit einem allgemeinen Radius r mit einem eingezeichnetem Dreieck. Dieses Dreieck hat die Eckpunkte A, B und M. Die dazu gehörigen Winkel sind α,β und ϕ.
Nun wollen wir herausfinden, wie groß der Winkel ϕ im Punkt M ist. Dazu schauen wir uns zunächst das an, was wir wissen:
Wir wissen, dass jeder Punkt auf dem Kreis den selben Abstand zum Mittelpunkt hat und zwar den Radius. Daraus folgt, dass die Strecken AM und BM gleich lang sind. Somit handelt es sich bei einem solchen Dreieck immer um ein gleichschenkliges Dreieck! Wir wissen von vorherigen Themen, dass die Basiswinkel in einem gleichschenkligem Dreieck immer gleich groß sind! Das heißt α = β!
Diese Aussagen nutzen wir nun für folgende Abbildung, die wir für die entgültige Beweisführung brauchen an.
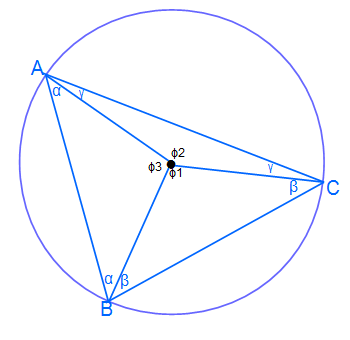
In dieser Abbildung sehen wir die Erweiterung der vorherigen Abbildung. Nun haben wir drei Punkte auf dem Kreis A, B und C. Alle Punkte sind gleich weit vom Mittelpunkt M entfernt. Wir haben drei gleichschenklige Dreiecke AMB, BMC und CMA. Die Basiswinkel der einzelnen Dreiecke sind immer gleich groß, so dass wir die gleichgroßen Winkel auch gleich benannt haben.
Nun nutzen wir all diese Informationen, um die Aussage des Kreiswinkelsatzes zu beweisen.
Beweis
Die Aussage des Kreiswinkelsatzes ist: „Der Mittelpunktswinkel ist doppelt so groß wie die Randwinkel“. Dies wollen wir nun beweisen. Die Aussage des Satzes als Formel wäre notiert: ϕ = 2α
Oben sind wir die Fakten durchgegangen, die wir durch unserer bestehenden Wissen kennen und diese wollen wir nun anwenden zum Beweis der Aussage.
1. Schritt: Winkelsummensatz im Dreieck AMB (vgl. Abb.)
α + α = 180°
2α + ϕ = 180° | -ϕ
2α = 180° – ϕ
2. Schritt: Winkelsummensatz im Dreieck ABC (vgl. Abb.)
α + α + β + β + γ + γ = 180°
2α + 2β + 2γ = 180°
3. Schritt: Einsetzen von 2α = 180° – ϕ und umformen
180° – ϕ + 2β + 2γ = 180° | -180°
– ϕ + 2β + 2γ = 0 | + ϕ
2β + 2γ = ϕ
2(β + γ) = ϕ
4. Schritt: β + γ = α (vgl Abb.)
ϕ = 2α
Somit haben wir bewiesen, dass die Aussage des Zentriwinkelsatzes gilt und der Mittelwinkel doppelt so groß ist, wie ein Randwinkel. Dies konnten wir nur durch unser vorheriges Wissen ermitteln und durch einsetzen und umformen der Formeln.
Diese neue Aussage können wir nun für Aufgabenstellungen nutzen und für weitere Erkenntnisse anwenden.
