Sehnentangentenwinkelsatz
Als weiteren Kreiswinkel haben wir den Sehnentangentenwinkel. Dieser wird auch durch einen eigenen Satz, Sehnentangentenwinkelsatz beschrieben und ist eine Erweiterung bis vorangegangenen Sätze.
Der Sehnentangenensatz besagt, dass der Sehnentangentenwinkel genauso groß ist wie der Umfangswinkel.
Diese Aussage lässt sich leicht mit den bisher durchgeführten Erläuterungen erklären.
Unser Lernvideo zu : Sehnentangentenwinkelsatz
Erklärung
Die Erklärung zum Sehnentangentenwinkelsatz basiert auf den bisherigen Erläuterungen.
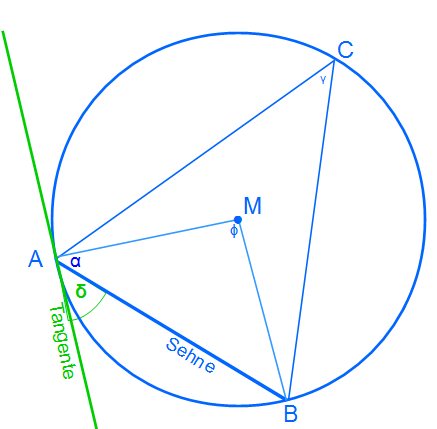
In der Abbildung sehen wir, wie die Tangente durch den Punkt A läuft. Der Punkt A ist ein Punkt der Sehne AB. Die Tangente läuft senkrecht, also im 90° Winkel zum Radius. Der Radius ist die Strecke AM. Wir wissen somit, dass die Winkel α + δ = 90°. Nun sagt der Sehnentangentenwinkelsatz, dass δ = γ.
Es gibt jeweils zwei Tangenten, eine durch Punkt A und eine durch Punkt B. Beide sind senkrecht zum Radius und beide Sehnentangentenwinkel sind somit gleich groß. Daher haben wir nur eine Tangente eingezeichnet.
Beweis
Nun beweisen wir mathematisch die Aussage dieses Satzes.
1. Schritt: Kreiswinkelsatz
ϕ = 2γ
2. Schritt: Winkelsumme des gleichschenkligen Dreiecks ABM ist 180°
α + α + 2γ = 180°
2α + 2γ = 180°
2(α + γ) =180°
α + γ = 90°
α = 90° – γ
3. Schritt: Einsetzen in Sehnentangentensatz
δ = 90° – α
δ = 90° – (90° – γ)
δ = γ
Somit haben wir bewiesen, dass der Sehnentangentenwinkel genauso groß ist wie der Umfangswinkel und somit auch halb so groß wie der Zentriwinkel ist.
