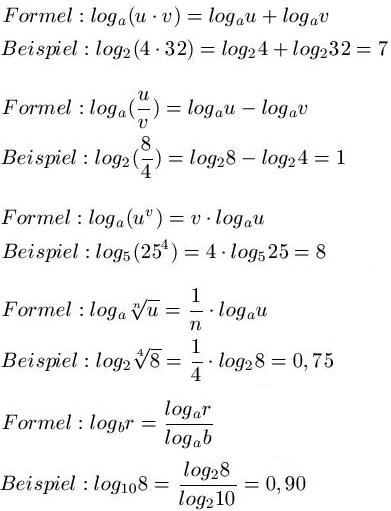Dekadischer Logarithmus
Der dekadische Logarithmus, auch Zehnerlogarithmus genannt, ist in der Mathematik der Logarithmus zur Basis 10.
Eigenschaften
►Man schreibt auch log10 a oder lg a.
►log a ist diejenige reelle Zahl, für die a = 10log a gilt
►log a existiert nur für a > 0, denn 10x > 0 für jedes x ∈ R.
►log 1 = 0, denn 100 = 1
►log x ist streng monoton wachsend, d.h. 0 < a < b ⇒ log a < log b.
►Für a ∈ (1, 10) gilt log a ∈ (0, 1)
►Für a ∈ (0, 1) gilt log a < 0, denn log a = − log a −1 = − log 1/a < 0, da 1/a > 1
►log a ist nach oben und nach unten unbeschränkt, denn für k ∈ Z gilt: a = log 10k =⇒ log a = k
►Die Berechnung eines Logarithmus ist also nichts anderes als die Bestimmung des Exponenten einer Potenz, mit anderen Worten: Logarithmen sind Exponenten
Wann ist ein Logarithmus nicht definiert?
- Der Logarithmus ist nicht definiert, wenn der Numerus den Wert Null hat, da keine Potenz zum Wert Null führt (ohne Berücksichtigung von Null hoch Null):
- loga0=n.d., denn ax≠ 0
Unser Lernvideo zu : Dekadischer Logarithmus
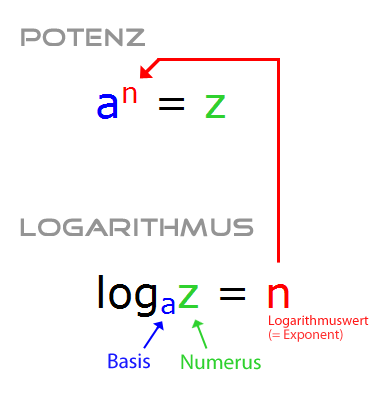
Die Grafik zeigt den Zusammenhang zwischen Potenz und Logarithmus
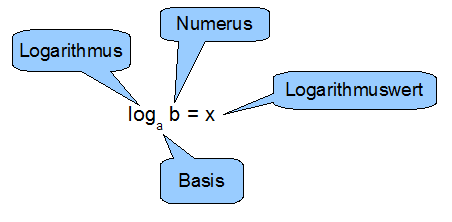
Abkürzung der Logarithmen: log, lg, ln, ld
Wahrscheinlich werdet ihr auch oft auf die Abkürzungen der Logarithmen treffen (im Zusammenhang mit der Basis). Die Kurzschreibweisenlauten:
Dekadischer Logarithmus (mit Basis 10) (auch „Zehnerlogarithmus“)
log10n = lg n
Logarithmus Naturalis (mit Basis e, Eulersche Zahl e = 2,718281828…) (auch „natürlicher Logarithmus“)
logen = ln n
Logarithmus Dualis (mit Basis 2) (auch „Zweierlogarithmus“) (wird auch als „binärer Logarithmus“ bezeichnet und mit „lb“ abgekürzt)
log2n = ld n
Beispiele
lg100000 = 5 , da 105=100000
lg0,001= -3 , da 10-3=0,001
Spezialfälle
log(10) =1 , da 101=10
10log(x)=x = log(10x)
Die Rechengesetze des Logarithmus