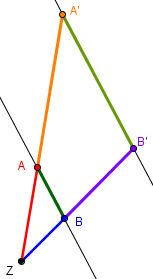
Zweiter Strahlensatz
Der zweite Strahlensatz schließt im Gegensatz zum ersten auch die parallelen Geraden mit ein. Er lautet:
![]()
Bei dem zweiten Strahlensatz müssen wir darauf achten, dass wir bei den Strecken der sich schneidenden Geraden immer bis zum Kreuzungspunkt Z rechnen müssen und nicht wie im ersten Strahlensatz mit den Teilstrecken AA‘ und BB‘ rechnen können.
Unser Lernvideo zu : Zweiter Strahlensatz
Beispiel 1
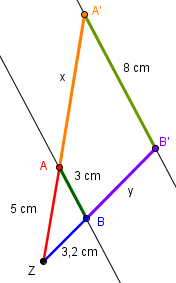
Wir sollen die fehlenden Größen x und y berechnen.
Berechnung von x
Wir beginnen mit x. Wir benötigen also eine Gleichung wo nur x als Unbekannte auftaucht. Wir müssen also den zweiten Strahlensatz wählen. Mit dem ersten Strahlensatz könnten wir nur eine Gleichung aufstellen, in der x und y unbekannt wären. Diese würde uns nicht weiterhelfen.
![]()
Wir setzen ein und erhalten:
![]()
Da wir bei der Strecke ZA‘ nur einen Teil kennen, müssen wir sie durch eine Addition ausdrücken (5 cm + x). Wir formen diese Gleichung nun um. Zunächst müssen wir das x aus dem Nenner holen. Dazu multiplizieren wir *(5 cm + x). Wir rechnen hier zunächst ohne Einheit, da dies etwas übersichtlicher ist.
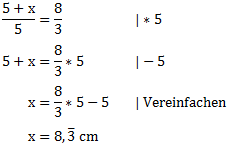
Alternativer Weg
Wir können es uns hier ein bisschen einfacher machen, indem wir die Ursprungsgleichung einfach umdrehen. Wir können auf beiden Seiten Zähler und Nenner vertauschen. Dann lautet die Ausgangsformel:
![]()
Wenn wir dann einsetzen und umformen ist der Weg deutlich kürzer, da das x schon im Zähler steht und wir es nicht multiplizieren müssen und ausklammern.
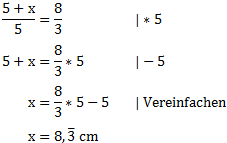
Wir bekommen auf diesem Weg dasselbe Ergebnis, der Rechenweg ist allerdings um einiges kürzer.
Berechnung von y
Genauso wie wir x berechnet haben, berechnen wir nun auch y. Dabei wählen wir den einfacheren Weg und wählen die Gleichung so, dass y im Zähler steht.
![]()
Wir setzen ein uns lösen die Gleichung:

Damit haben wir die beiden Unbekannten berechnet.
Beispiel 2
Etwas komplizierter wird es bei folgender Aufgabe:
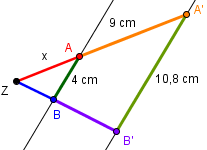
Auch hier sollen wir x berechnen. Wir benutzen diese Gleichung dafür:
![]()
Wir setzen ein und erhalten:
![]()
Bei dieser Gleichung haben wir nun an zwei Stellen x und müssen diese zusammenfassen. Es gibt mehrere Möglichkeiten dafür.
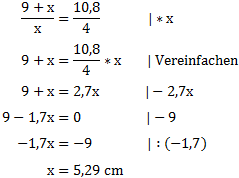
Alternativer Weg
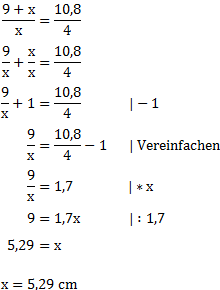
Da beide Wege etwa gleich aufwändig sind, ist es Geschmackssache welchen man geht.
