Multiplikation von Dezimalzahlen
Die schriftliche Multiplikation von Dezimalzahlen wird genauso gemacht wie die schriftliche Multiplikation von natürlichen Zahlen und ist uns somit bereits bekannt. Da die Faktoren nebeneinander geschrieben werden, ist es auch n icht wichtig, die Kommas untereinander zu schreiben, wie wir es bei der Addition oder Subtraktion machen.
Für die richtige Kommastelle im Ergebnis addieren wir alle Kommastellen zusammen, zählen diese von hinten ab und tragen das Komma dann ein.
Wir sehen uns wieder einige Besipiele an, um es darzustellen.
Lerntool zu Multiplikation von Dezimalzahlen
Beispiel 1:
Wir multiplizieren 56,23 mit 3,25.
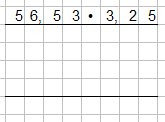
Wie in der Abbildung und wie wir es auch von den natürlichen Zahlen kennen, schreiben wir die Faktoren zunächsten nebeneinander. Wir lassen dann drei Zeilen frei für die Rechnung und eine für mögliche Überträge.
Wir multiplizieren zunächst:

Nun haben wir wie gewohnt ausmultiplizert. Was wichtig ist, es werden noch keine Kommas eingesetzt. Dies wird ganz zum Schluss gemacht. Nun werden als nächstes die Zahlen addiert.
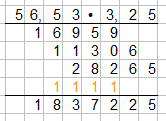
Nun haben wir die zuvor multiplizierten Produkte addiert und die Überträge in orange eingetragen. Als letzten Schritt folgt nun das Einsetzen des Kommas. Die Anzahl der Nachkommastellen ergibt sich durch die Summe aller Nachkommastellen der Multiplikation. Das heißt in unserem Fall von 56,53 • 3,25 haben wir 2+2 = 4 Nachkommastellen und die zählen wir nun von hinten in unserem Ergebnis ab und tragen es ein:
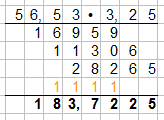
Somit erhalten wir als Produkt: 183,7225
Beispiel 2:
Wir multiplizieren 2,5 mit 6,008. Zunächst werden die Zahlen wir gehabt eingetragen und ohne Kommas zu setzen ausgerechnet:
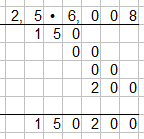
Wieder wurde Zahl für zahl multipliziert und untereinander geschrieben. Danach wurde alle Produkte addiert. Wer möchte kann sich zur Übersicht in die leeren Stellen Nullen schreiben. Die verändert das Ergebnis nicht. Da sieht es wie folgt aus:
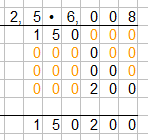
Wir sehen nun in den Lücken eingefügte Nullen. Dies kann zur helfen, verändert aber das Ergebnis nicht.
Nun setzen wir noch das Komma ein. 2,5 und 6,008 haben gemeinsam 4 Nachkommstellen. Diese zählen wir wieder von hinten ab und setzen das Komma richtig ein:
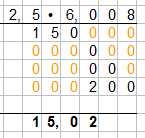
Da wir die Nullstellen am Ende einer Dezimalzahl wegfallen lassen können ergibt sich:
2,5 • 6,008 = 15,02
Beispiel 3:
Nun kann es auch vorkommen, dass wir Zahlen multiplizieren von denen eine kleiner ist als 1, dann wird das Produkt kleiner als der andere Faktor!
Z.B.: 18,6 • 0,5
dieses berechnen wir zunächst wie gehabt:
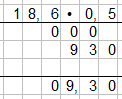
Das Ergebnis ist 09,30, da wir insgesamt zwei Nachkommastellen haben. Nun können wir nie vorderste und hinterste Null wegfallen lassen ohne das Ergebnis zu verändern und erhalten: 18,6 • 0,5 = 9,3
Hier sehen wir, dass das Produkt kleiner ist als der erste Faktor. Dies liegt daran, dass der 2. Faktor kleiner ist als Eins! Dieses wird euch öfter begegnen und ihr dürft euch dabei nicht wundern. Nur wenn beide Faktoren größer oder geich sind als Eins, dann wird das Produkt größer.
Nun haben wir auch die Multiplikation von Dezimalzahlen gemacht, was zum Glück nicht schwer ist.
