Gradmaß und Bogenmaß

Gradmaß

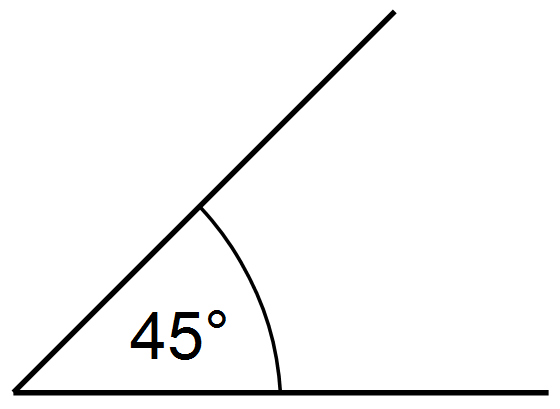
In der Schule lernt man zunächst das Gradmaß kennen. Hier beträgt der Vollwinkel („einmal ganz rum“) α = 360° und 1° ist dementsprechend der 360. Teil eines Vollwinkels, also auch der 360. Teil eines Kreises. Für das Vorliegen des Gradmaßes können folgende Hinweise verwendet werden:

• der Winkel ist mit dem °-Zeichen (Grad-Zeichen) angegeben
• der Winkel ist oft mit einem griechischen Buchstaben (α, β, γ…) bezeichnet
• es werden geometrische Berechnungen an Körpern wie Dreiecken, Vierecken etc. vorgenommen

 Beispiel

Bogenmaß (Radiant)

Die Angabe eines Winkels im Bogenmaß bezieht sich auf die Länge des dazugehörigen Kreisbogens im Einheitskreis. Der Einheitskreis ist ein Kreis mit dem Radius r = 1. Der Vollwinkel entspricht dem Gesamtumfang des Einheitskreises und beträgt demnach 2π. Dass die Winkelangabe im Bogenmaß vorliegt, kann man an folgenden Anhaltspunkten erkennen:

• keine Einheit vorhanden (bzw. wird die Einheit „rad“ in der Regel weggelassen)
• π kommt oft vor
• man zeichnet einen Funktionsgraphen

Beispiel

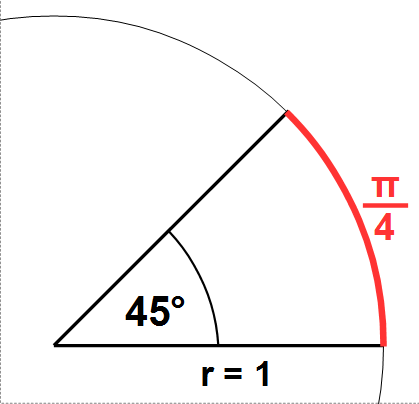
Hier ist nur der betreffende Ausschnitt des Einheitskreises zu erkennen. Ein Winkel von 45° im Gradmaß entspricht ¹/₄ π im Bogenmaß.

Umrechnung

360° im Gradmaß entsprechen 2π im Bogenmaß. Somit erfolgt die Umrechnung per Dreisatz:

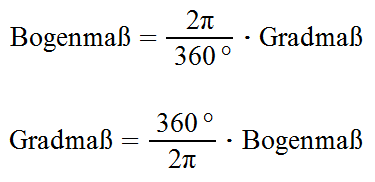
Beispiel

Ein Winkel von 90° soll im Bogenmaß angegeben werden.

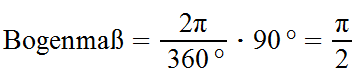
Ein Winkel von π soll ins Gradmaß umgewandelt werden.

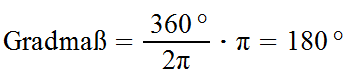
Auf der folgenden Tabelle sind die wichtigsten Winkel in Grad- und Bogenmaß dargestellt.

0

Taschenrechner richtig einstellen

Bei den meisten Taschenrechnern ist die standardmäßige Einstellung das Gradmaß, welches mit DEG (=degree) angegeben wird. Ist jedoch das Bogenmaß gegeben, ist unbedingt auf RAD (=radian) zu wechseln.
Hier werden oft Fehler gemacht und es kommt zu großen Unterschieden im Ergebnis, weshalb vorher genau zu überlegen ist, welche Einstellung zur Aufgabenstellung passt.

Unser Lernvideo zu : Gradmaß und Bogenmaß