Parallelität eines Vektors
Eine Menge von Vektoren ist linear abhängig, wenn man eine Linearkombination von ihnen bilden kann, die den Nullvektor ergibt und nicht trivial ist (trivial wäre, einfach von allen Vektoren das Nullfache zu nehmen). Geht das nicht, so sind sie linear unabhängig.
Woran erkenne ich, ob zwei Vektoren parallel sind?
Haben zwei Geraden denselben Richtungsvektor, so sind diese parallel.
Liegt der Stützvektor der eines Vektors auf der parallelen Vektor, so sind die Geraden parallel und zugleich identisch.( Um dies herauszufinden, ist eine Punktprobe notwendig)
Vektoren sind nicht an einen Ort gebunden, sie lassen sich beliebig verschieben. Deshalb greifen hier solche Wörter wie „parallel“ und „identisch“ nicht, sondern man benutzt den Begriff „kollinear“, was soviel wie „auf einer Linie liegend“ bedeutet
Lineare Abhängigkeit im zweidimensionalen Raum
Verfahren
Zwei Vektoren sind im R2 genau dann linear abhängig, wenn sie Vielfache voneinander sind. Unser Rechenansatz lautet aus diesem Grund
a=k⋅b
Beispiel
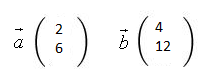
Wenn es ein k (ungleich Null!) gibt, das das Gleichungssystem löst, so sind die Vektoren linear abhängig.
4= k*2 ⇒ k=2
12= k*6 ⇒ k=2
Wenn es ein k (ungleich Null!) gibt, das das Gleichungssystem löst, so sind die Vektoren linear abhängig also Parallel
Eigenschaften von Vektoren im R2
- Vektoren sind im R2 genau dann linear abhängig, wenn sie parallel sind.
- 3 (oder mehr) Vektoren sind im R2 stets linear abhängig
Drei Vektoren heißen linear abhängig, wenn es drei Zahlen λ1, λ2 und λ3 gibt, die nicht alle gleich Null sind!
