Komplanarität eines Vektors
♦Die Komplanarität von drei Vektoren bezieht sich auf die Lage zueinander bzw. in den Ebenen.
♦Komplanarität bezeichnet drei Vektoren, die alle in der gleichen Ebene liegen und sich dieses gemeinsame geometrische Merkmal teilen.
♦Wenn drei Vektoren komplanar sind, können sie durch Pfeile in derselben Ebene beschrieben werden. Das bedeutet für die Rechnung, dass einer von den Vektoren eine Linearkombination der beiden anderen sein muss
Tabellarische Übersicht
| Gerade/Ebene | alle Richtungsvektoren komplanar | Vektoren sind nicht Komplanar |
| Punkt(e) gemeinsam | Gerade liegt in Ebene | Gerade durchstößt Ebene im „Spurpunkt“
Winkelberechnung |
| kein Punkt gemeinsam | Gerade parallel zur Ebene.
Abstandsberechnung |
nicht möglich |
| Gerade/Ebene | Vektor |
| fest | beliebig verschiebbar |
| parallel, schneidend, windschief | kollinear/ komplanar |
Vorgehensweise
Mit 3 Vektoren berechnen
♦Wenn man für drei Vektoren berechnet, ob sie alle das Merkmal der Komplanarität miteinander teilen, muss man also prüfen, ob die Vektoren in der gleichen Ebene liegen.
♦Dafür kann man eine Gleichung aufstellen, in der man davon ausgeht, dass zwei der Vektoren in einer Ebene liegen. Dann setzt man sie mit dem dritten gleich und überprüft, für welche Vektoren das Gleichungssystem erfüllt ist. Sind alle erfüllt, liegen auch alle Vektoren in einer Ebene und sind komplanar.
♦Man kann einen Vektor vor das Gleichzeichen setzen und die beiden anderen jeweils mit einem variablen Faktor davor. (Diese Faktoren dürfen nur reelle Zahlen sein)
♦Lassen sich Faktoren finden, mit denen beide Vektoren so multipliziert und diese Ergebnisse addiert werden können, dass als Ergebnis der dritte Vektor herauskommt, gelten sie als komplanar, da sich eine Linearkombination bilden lässt.
♦Auch kann man alle Vektoren gleich Null setzen und jeweils mit einer reellen Zahl außer dreimal der Null kombinieren. Wenn sich diese Gleichung mit einem sogenannten Spatprodukt auflösen lässt, sind sie ebenfalls komplanar.
Beispiel
Gegeben haben wir folgende Vektoren
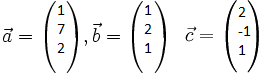
Wir untersuchen diese Vektoren also auf lineare Unabhängigkeit. Das heißt die linearkombination zweier Vektoren, darf den dritten nicht ergeben. Hier also
r·[1, 7, 2] + s·[1, 2, 1] = [2, -1, 1]
⇒Die ersten beiden Zeilen geben folgendes Gleichungssystem
r + s = 2
7r + 2s = -1
Die Lösung wäre hier r = -1 ∧ s = 3
Setzte ich das in die dritte Gleichung ein
2r + s = 2*(-1) + 3 = 1
So ist die dritte Gleichung auch erfüllt und die Vektoren sind somit linear abhängig bzw. komplanar.
Merke: Sehr einfach ist es auch einfach die Determinante der drei Vektoren zu berechnen.
DET([1, 7, 2; 1, 2, 1; 2, -1, 1]) = 0
Wir können die Determinante auch als Spatprodukt dieser 3 Vektoren auffassen. Die Determinante entspricht damit auch dem Rauminhalt des von den Vektoren aufgespannten Raumes. Ist dieser Null wird nur eine Ebene aufgespannt und die Vektoren sind komplanar.
