Lineare Abhängigkeit 2 Vektoren
Linear abhängig im 2D-Raum sind
● Zwei kollineare Vektoren (ein Vektor ist ein Vielfaches des anderen)
● Drei oder mehr Vektoren
Eine Menge von Vektoren heißt linear abhängig, wenn sich mindestens ein Vektor als Linearkombination der anderen darstellen lässt.
Eigenschaften
♦2 Vektoren sind im R2 genau dann linear abhängig, wenn sie parallel sind.
♦3 (oder mehr) Vektoren sind im R2 stets linear abhängig.
♦In der Ebene R2 sind drei Vektoren immer voneinander linear abhängig
♦Im Raum R3 sind vier Vektoren immer voneinander linear abhängig
Zwei Vektoren sind genau dann linear abhängig, wenn sich der Nullvektor durch eine Linearkombination der Vektoren erzeugen lässt,
λ1a1→+λ2a2→=0
in der mindestens einer der Koeffizienten λ1 bzw. λ2 ungleich Null ist
Beipspiel
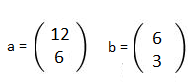
12 = λ* 6 → λ = 2
6 = λ *3 → λ = 2
Da es ein λ (ungleich Null) gibt, sind die Vektoren Vielfache voneinander und somit linear abhängig!!
Beispiel 2
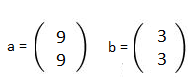
9 = λ* 3 → λ = 3
9 = λ *3 → λ = 3
Linear Abhängig!
