Division von Funktionen ableiten
„Division von Funktionen ableiten“ geht zurück auf den Quotientenregel. Was das genau war und funktioniert, darauf kommen wir später zurück. Zuerst wollen wir einmal klären was Quotientenregel ist und wann wir es benutzen.
Die Quotientenregel ( auch Division von Funktionen ableiten genannt) gibt an, wie du eine Funktion ableiten kannst, die als Quotient zweier Funktionen dargestellt ist. Solche Funktionen haben die Form
![]()
Die Funktionen u(x) und v(x) sollen dabei differenzierbar sein. Dann ist auch f(x) differenzierbar und die
Ableitung f´(x) ist
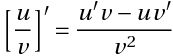
Die Formel kann auf dem ersten Blick sehr schwer aussehen. Doch ist es eigentlicht nicht….
Wir schauen uns noch einmal die Formel an.
![]()
Man kann diese Formel natürlich auch kürzen und so hinschreiben
![]()
Das ganze wollen wir nun mit einem Beispiel veranschaulichen. Dazu nehmen wir folgende Funktion,
![]()
Am einfachsten ist es, wenn Ihr zuerst die Funktion aufteilt in „u“ und „v“. Dann ist auch das Ableiten hinterher nicht so schwer
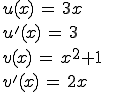
Nachdem wir nun die Funktion aufgeteilt haben, wollen wir nun nach der Formel ableiten. Dafür setzen wir einfach die Zahlen ein
![]()
Merke
►Du verwendest diese Regel wenn dein Funktionsterm ein Bruch ist
►Notiere dir immer Zähler und Nenner sowie deren Ableitungen
►Als Merkregel für den Zähler lässt sich die Kurzform „NAZ minus ZAN“ für „Nenner („N“) mal Ableitung des Zählers („AZ“)minus Zähler („Z“) mal Ableitung des Nenners („AN“))“ benutzen
►Eine weitere Merkregel für den Zähler ist die Kurzform „AZN minus ZAN“: Ableitung des Zählers („AZ“) mal Nenner („N“) minusAbleitung des Nenners („AN2) mal Zähler („Z“)
