Summenregel bei Ableitungen
Summenregel
Die Formel lautet
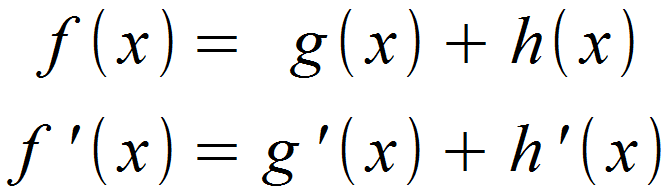
Bedeutung: Eine Summe wird abgeleitet, indem man jeden Summanden für sich ableitet und die Ableitungen addiert
►Obwohl die Summenregel dem Namen nach für Summen angewendet wird, gilt sie auch bei Subtraktion von mehreren Funktionsgliedern. Man kann sie dann auch als „Differenzenregel“ bezeichnen.
Die Summenregel besagt, dass bei der Ableitung einer Funktion, die sich durch Addition und/oder Subtraktion mehrerer Funktionen zusammensetzt, gliedweise differenziert werden darf. Nehmen wir z.B. die Funktion
f(x) = 8x² +2x. Diese setzt sich aus g(x) = 8x² und h(x)=2x zusammen. Die Ableitung der Funktion f(x) ist nun die Summe der Ableitungen von g(x) und h(x) also 16x+2
Beispiel
Gegeben haben wir die Funktion ⇒ f(x)= x2+ sin(x)
Gesucht ist die 1 Ableitung und die Ableitung an der Stelle x0=π/2
►Rechnung:
Wir wollen mit der Summenregel nun die erste Ableitung bilden
und erhalten als Lösung f`(x)=2x+cos(x) ⇒ Merke! Ableitung von Sinus ist Cosinus
Ableitung an der Stelle x0 berechnen
Wir setzen für die X-Werte nun π/2 ein
⇒ f`(x0)=2x0+cos(x0)
⇒f`(x0)=2*(π/2) +cos(π/2) = π +0= π
Die Ableitung an der Stelle π/2 beträgt π! Also ist π unsere Lösung!
Weitere Beispiele zur Summenregel
f(x)= x5 + x5
f`(x)= 5x + 5x
f(x)=16x6+5x4
f`(x)=96x5 +20x3
f(x)=2x3+7x
f`(x)=6x2+7
f(x)=3x2+x
f`(x)=6x+1
