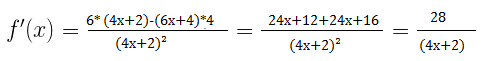Bruch ableiten
Ableitung Definition
Eine Ableitung hilft dir, die Steigung eines Graphen an einer beliebigen x-Koordinate zu bestimmen.
Du bildest die Ableitung und setzt in diese dann den x-Wert ein. Das „Ergebnis“ ist die Steigung.
Mit der Tangente hat es deshalb zu tun, weil die Tangente an einem „kurvenförmigen“ Graph immer dieselbe Steigung wie der Graph an der Stelle hat, an dem die Tangente anliegt.
Die Steigung des Graphs ist also mit der Steigung der Tangente identisch.
Burch Definition
Ein Bruch wird durch Zähler, Nenner und Bruchstrich definiert. Der Bruchstrich hat hierbei die gleiche Bedeutung wie „geteilt durch“ Unechte Brüche lassen sich in einen gemischten Bruch umwandeln und umgekehrt. Man erhält den Kehrwert eines Bruches, indem man Zähler und Nenner vertauscht.
Brüche leitet man immer mit Quotientenregel ab!
Quotientenregel ist immer dann anzuwenden, wenn sowohl im Zähler als auch im Nenner einer Funktion ein x vorkommt z.B
![]()
►Die Quotientenregel ist eine grundlegende Regel der Differentialrechnung. Sie führt die Berechnung der Ableitung eines Quotienten von Funktionen auf die Berechnung der Ableitung der einzelnen Funktionen zurück.
►Die quotientenregel verwendet man immer bei gebrochenrationalen funktionen (also bei Brüchen)
►Die Quotientenregel ist eine kombination aus Produkt und Kettenregel
Im Gegensatz zur Produktregel kommt es bei der Quotientenregel im Zähler auf die Reihenfolge der Terme an, da die Subtraktion nicht kommutativ (umstellbar, vertauschbar) ist! Als Eselsbrücke kannst du folgende einfache Merkregel benutzen
1. Merkregel ⇒ „NAZ minus ZAN“
Als Merkregel für den Zähler lässt sich die Kurzform „NAZ minus ZAN“ für
„Nenner („N“) mal Ableitung des Zählers („AZ“) minus Zähler („Z“) mal Ableitung des Nenners („AN“))“ benutzen.
2. Merkregel ⇒ „AZN minus ANZ“
Eine weitere Merkregel für den Zähler ist die Kurzform „AZN minus ZAN“:
Ableitung des Zählers („AZ“) mal Nenner („N“) minus Ableitung des Nenners („AN2) mal Zähler („Z“)
Beispiel Rechnung
Die Formel für die Ableitung lautet wie folgt
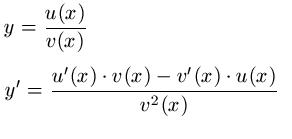
Unser Beispiel
Wir schreiben uns zuerst heraus was g(x) und was h(x) ist
►g(x)= 6x+4, dann ist die erste Ableitung g`(x)= 6
►h(x)=4x+2, dann ist die erste Ableitung h`(x)= 4
Jetzt setzen wir in die Formel ein