Aufleiten Substitution
Die Integration durch Substitution wird immer dann angewendet, wenn ein Faktor des Integranden die Ableitung der inneren Funktion des anderen Faktors ist. Als Faustregel kann gesagt werden: Substitution ist beim Integrieren immer dann angezeigt, wenn man die Kettenregel benutzen würde, um den Term abzuleiten.
Vorgehensweise:
♦Substitution, Ableitung und Umstellen
♦Substitution bei der Integralaufgabe durchführen
♦Integral lösen
♦Rücksubstitution durchführen
Merkregel 1: Die Stammfunktion / das unbestimmte Integral einer Funktion ist wieder eine Funktion bzw. eine Menge von Funktionen!
Merkregel 2: Das bestimmte Integral einer Funktion ist eine Zahl!
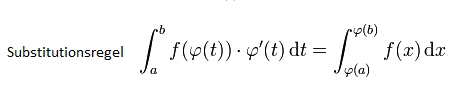
→ Bei φ handelt es sich um das kleine „Phi“ des griechischen Alphabets!
Beispiel 1
Gegeben haben wir folgende Funktion ![]()
•Durch Substitution haben wir u= x+1
•Nun differenzieren wir die Substitution ![]()
• Jetzt lösen wir nach dx auf und erhalten dafür dx= 1du
• Als integral umgeschrieben haben wir ∫ u2 du
• Nun differenzieren wir die Grenzen des Integrals, indem wir unser u=x+1 in die obere und untere Grenze einsetzen
Untere Grenze: u= -1+1=0
Obere Grenze: u= 2+1=3
Damit lautet das Integral ![]()
folgt: ![]()
Beispiel 2
![]()
•Substitution u= x+2
•![]() → umgestellt nach dx: dx=1du
→ umgestellt nach dx: dx=1du
•Integrattionsgrenzen
Untere Grenze: u= 0+2=0
Obere Grenze: u= 2π+ 2
•Somit lautet das Integral
![]()
•Integral durchführen ![]()
