Aufleitung Summenregel
Das Auffinden einer Stammfunktion heißt Integration.
Eine Stammfunktion F einer Funktion f(x) ist bis auf eine Integrationskonstante C genau bestimmt. Das wird deutlich, wenn man die Stammfunktion ableitet. Denn bei diesem Vorgang verschwindet die Konstante C. Es gibt folglich eine unbestimmte Menge an Stammfunktionen zu einer Funktion f(x). Daher nennt man die Menge der Stammfunktionen zu einer Funktion f(x) auch unbestimmtes Integral.
Einfach ausgedrückt → Man kann Stammfunktionen als „Mütter oder Väter der Funktion“ bezeichnen und die Ableitung von einer Funktion als „Kinder der Funktion“, sie sind also die „Enkel der Stammfunktionen“. Dieser Vergleich trifft die Situation im „Reich der Funktionen“ aber nicht ganz, denn eine Funktion hat höchstens eine Ableitung, aber unendlich viele Funktionen als Stammfunktionen.
→statt „aufleiten“ sagt man meist „integrieren
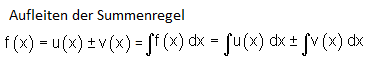
Zwischen Integral- und Stammfuntkion besteht folgender Zusammenhang:
Jede Integralfunktion ist eine Stammfunktion, aber nicht umgekehrt. Alle Stammfunktion F zu f unterscheiden sich durch eine additive Konstante c. D. h. kennt man eine Stammfunktion, so kennt man alle.
Merksätze die du wissen und auswendig lernen solltest!
♦Das Integral über eine Summe ist gleich der Summe der Integrale über die Summanden
♦Hauptsatz der Differential und Integralrechnung : Die „Umkehrbarkeit“ der Differential und Integralrechnung: Das Integral von f(x) ergibt diejenige Funktion F(x), die abgeleitet wieder f(x) ergibt.
♦Die gegebene Funktion f(x) ist ihrerseits Ableitung einer Funktion F(x). F(x) heißt Stammfunktion von f(x).
♦Das Absolute Glied c (Integrationskonstante) in der Stammfunktion ist nicht bestimmbar und wird als Platzhalter (c) angegeben
Beispiel 1
f(x)= x2 +x +1
Integration → ∫ f(x) dx = ∫ x2dx + ∫x dx + ∫1 dx = x3/3 +x2/2 +x +C Lösung!
Beispiel 2
F(x)= ∫ 3x2 – ex + 4dx
→Jetzt einzelne Summanden integrieren
∫ 3x2 = x3
∫ ex = ex
∫ 4dx = 4x
→ Jetzt wieder aufsummieren ergibt = x3– ex +4x
→ Weil es hier um ein unbestimmtes Integral handelt, muss noch die Integrationskonstante C dazu
= x3 – ex +4x +C Lösung!
