Stammfunktion
Bei der Differentialrechnung haben wir bereits gelernt, wie man Funktionen ableitet. Was aber, wenn wir nur die Ableitung einer Funktion vorliegen haben? Wir müssen das Gegenteil der Differentialrechnung durchführen, die sogenannte Integralrechnung. Das Ergebnis dieser Integration, auch Aufleitung genannt, wird als Stammfunktion bezeichnet.
Unter der Stammfunktion einer Funktion f (x) versteht man die Funktion F (x), deren Ableitung F '(x) mit f (x) übereinstimmt. Die Stammfunktion F (x) ist demnach die Aufleitung von f (x). Mathematisch stellt man diesen Sachverhalt foglendermaßen dar.
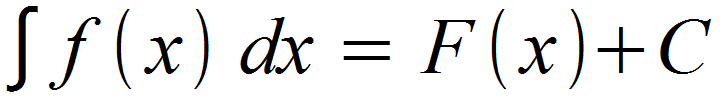
Auf das Integralzeichen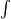 
folgt die aufzuleitenden Funktion f (x) sowie die Kennzeichnung, nach welcher Variable aufgeleitet werden soll. In der Regel ist dies x, also wird dx hinzugefügt. Man erhält die allgemeine Stammfunktion F (x) und eine Konstante C. Solche Integrale ohne Grenzen werden auch „unbestimmtes Integrale“ genannt
Es gibt zu jeder stetigen Funktion f (x) eine Stammfunktoin F (x). Stetigkeit bedeutet, dass in den Funktionswerten keine Sprünge vorliegen, es also zu jedem x– auch einen y-Wert gibt.
Unser Lernvideo zu : Stammfunktion
Die Konstante C
Zunächst ist es hilfreich sich vor Augen zu halten, dass das Aufleiten (Integrieren) als Gegenteil vom Ableiten (Differenzieren) anzusehen ist. Wie wir nun gelernt haben, ist F (x) die Stammfunktion von f (x). Ebenso ist f (x) auch die Stammfunktion von f '(x) und f '(x) wiederum die Stammfunktion von f “(x). In die andere Richtung gedacht ist f (x) natürlich die Ableitung von F (x) und, wie noch aus der Differentialrechnung bekannt, f '(x) die Ableitung von f (x).
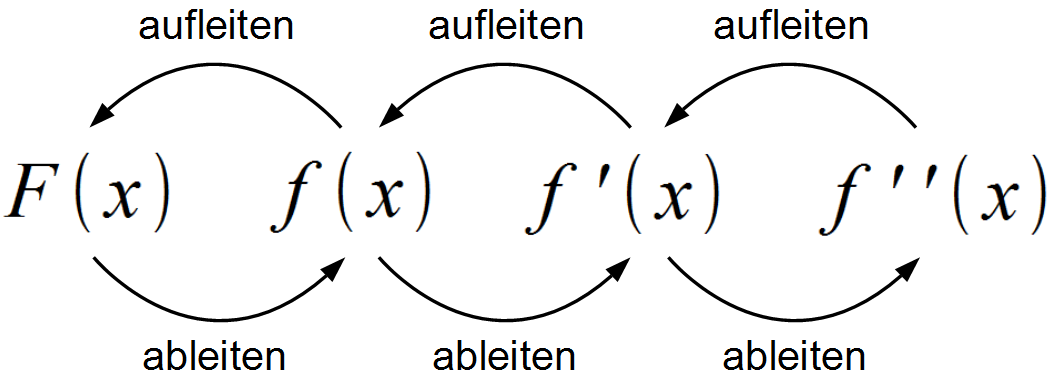
Zur Kontrolle ist es also möglich, die durch Integrieren erhaltene Stammfunktion wieder abzuleiten und zu prüfen, ob das Ergebnis der ursprünglichen Funktion entspricht.
Betrachten wir als konkretes Beispiel die Funktion f (x) = 2·x. Diese soll durch Ableiten einer gesuchten Stammfunktion F (x) erhalten werden.
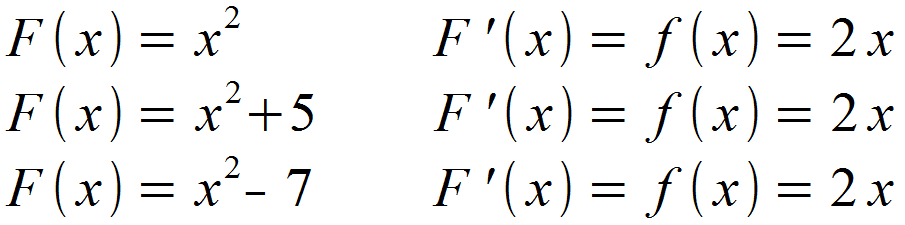
Wie man sieht, unterscheiden sich die genannten Stammfunktionen lediglich durch eine Konstante, die mit C gekennzeichnet und Integrationskonstante genannt wird. In der ersten Funktion ist sie ebenfalls vorhanden, nimmt allerdings den Wert 0 an. Die Konstante ist generell unabhängig von x und fällt dadurch beim Ableiten weg. Somit gibt es unendlich viele Möglichkeiten für die Integrationskonstante und dementsprechend auch unendlich viele Möglichkeiten für die Stammfunktion. Die Variable C berücksichtigt also, dass möglicherweise ein Wert durch das Ableiten verloren gegangen ist.
Interessante Fragen und Antworten zu Stammfunktion
Was müssen wir jedoch tun, wenn die Ableitung gegeben und die Stammfunktion gesucht ist? |
| Die Integralfunktion befasst sich vor allem damit, eine Berechnung der Stammfunktion durchzuführen. Ist bei einer Aufgabe, die Funktion gegeben und die Stammfunktion wird gesucht, dann muss als erstes eine Ableitung der Funktion vorgenommen werden. Um diesen Vorgang zu erleichtern, kann es hilfreich sein einige bekannte Stammfunktionen auswendig zu lernen. Zum Beispiel die der Wurzel, des Sinus oder Kosinus. Bei vielen Übungen trifft man aber, auf schwierige Funktionen, bei denen das Ableiten nicht so einfach ist. Um bei solchen Funktionen die Berechnung der Stammfunktionen durchzuführen, können die Integrationsregeln behilflich sein. Hierzu gehören die Potenzregel, Faktorregel, Summenregel, partielle Integration und die Differenzregel. |
Wie bestimmt man eine Stammfunktion einer Exponentialfunktion? |
| Beginnen wir mit der natürlichen Exponentialfunktion f(x) = e^x. Wir wissen bereits, dass deren Ableitung identisch mit der Funktion ist, demnach lässt sich auch die Stammfunktion einfach berechnen: ?e^x dx = e^x + c wobei c aus RAls nächstes betrachten wir eine Funktion mit einer anderen Basis als e, also f(x) = a^x. Die zugehörige Stammfunktion sieht wie folgt aus: ?a^x dx = 1/lna · a^x + c Im Falle eines linearen Exponenten bei Basis e, also f(x) = e^ax+b, berechnet sich die Stammfunktion so: Beispiele: Bestimme alle Stammfunktionen von f(x) = 3^x Bestimme alle Stammfunktionen von f(x) = e^3x-2 |
Wie bestimmt man eine Stammfunktion einer ganzrationalen Funktion? |
| Eine ganzrationale Funktion wird auch Polynom genannt. Diese ganzrationale Funktion zeichnet sich durch folgende Merkmale aus: Sie ist die Summe von Vielfachen von Potenzen. Die höchste Exponent aller Potenzen in diesem Polynom nennt sich Grad des Polynoms. Nachdem wir nun geklär haben, as eine ganzrationale Funktion ist, rufen wir uns in Erinnerug, was eine Stammfunktion ist. Die Stammfunktion ist nämlich die Umkehr (oder auch Aufleitung) der gegebenen Funktion, welche im Umkehrschluss die Ableitung der Stammfunktion ist. Da wie bereits erwähnt eine ganzrationale Funktion ein Polynom ist, erhalten wir eine Gleichung, die in etwa wie folgt aussieht:f (x) = 5x + 3x hoch 2 + 8x hoch 3 Betrachten wir nun die Aufleitungsregeln: Eine Potenz wird abgeleitet, indem der Exponent mit 1 addiert wird und durch den neuen Exponenten dividiert wird. Der Faktor bleibt konstant. Zu der Aufleitung selbst wird zum Schluss die r Konstante C hinzu addiert. Beachten wir diese Regel, können wir die Funktion wie folgt aufleiten: 5x entspricht aufgeleitet (5 mal x hoch 2/2 + C) F (x) = 5 mal x hoch 2/2 + C + 8 mal x hoch 4/4 + C |
Wie bestimmt man eine Stammfunktion einer Logarithmusfunktion? |
| Die Frage „Wie bestimmt man eine Stammfunktion einer Logarithmusfunktion?“ beantwortet sich einfach über die Formel der Logaritmusberechnung. So einfach kann die Frage beantwortet werden, wenn man die das Tool Stammfunktionf (x) = l ogax
Bei der Stammfunktion wird das Integral einer Logarithmus Funktion gesucht. Mit entsprechender partieller Integration wird hier integriert und diese Funktion in der Ableitung nennt man Produktintegration. Für eine Produktintegration benötigt man als Basis ein Produkt um es dann in der Stammfunktion in den Logarithmus zu integrieren. Genau genommen handelt es sich hier jetzt um die partieller Integration. Wichtig ist dabei die Wahl der Funktionen, denn passiert hier ein Fehler so steigert sich der entsprechende Aufwand in der Berechnung. Hier die entsprechende Formel g'(x) = 1 und f(x) = ln(x). Jetzt kann man mit der Ableitung der Stammfunktion beginnen. Beziehungsweise die Integration beginnt mit der Ableitung von f(x) und g(x) in die Formel. Der nächste Arbeitsschritt ist die eigentlichen Integration und daraus ergibt sich ein Integral , das von x/x zu 1 gekürzt wird. Damit ist das Integral entsprechend berechnet und die Formel ist entsprechend ergänzt und damit vervollständigt. So kann die Frage genau entsprechend beantwortet werden und das ergibt sich aus dieser Arbeitsweise genau. |
Wie bestimmt man eine Stammfunktion einer Polynomfunktion? |
| Die Frage; „Wie bestimmt man eine Stammfunktion einer Polynomfunktion?“, ist über die Erklärung der Polynomfunktion und die Darstellung des Polynom zu erklären. Zur Beantwortung braucht man eine Formel.Die Mathematik beschreibt das Polynom als mehrarmig und eine endliche Summe eines Vielfachen von entsprechenden Potenzen. Dazu muss man wissen, dass diese Potenzen mit natürlichen Exponenten zusammen bezeichnet werden. In der Beantwortung der Frage muss zunächst das Polynom erklärt werden. Polynomfunktion und Polynome treten in unterschiedlichen Aufgabenbereichen der Berechnungen auf. So werden Polynomfunktion und deren Berechnung in der Physik und der Mathematik gleichermaßen verwendet. Die Beantwortung der Bestimmung einer Polynomfunktion richtet sich auch nach diesen Disziplinen und den unterschiedlichen Polynomen. Zudem müssen in der Betrachtung der Stammfunktion im Kontext zur Polynomfunktion auch entsprechende Potenzenreihen hinzugezogen werden.
Auch die Polynomfunktion muss erst einmal funktionell erläutert werden. Nur die Formel allgemein anzuwenden wäre zu einfach, denn die Polynomfunktion bildet einen Rechenschritt in der abstrakten Algebra. So ist noch wichtig das ein Polynom ein Element des Polynomrings ist. Vergleichbar ist die Polynomfunktion mit der ganzrationalen Funktion in der Mathematik. Zur Beantwortung der Frage nutzt man einfach die Formel der Stammfunktion für Polynomfunktionen: Das ergibt die Antwort zur Eingangs gestellten Frage. |
Wie bestimmt man eine Stammfunktion einer Potenzfunktion? |
| Eine Stammfunktion eines Produktes wir mit Hilfe der sogenannten Kettenregel ermittelt. Steht vor einer verketteten Funktion die Ableitung der inneren Funktion als Faktor, so erhält man eine Stammfunktion dieses Produktes, indem man eine Stammfunktion der äußeren Funktion dieser verketteten Funktion bildet. Die innere Ableitung wird dabei nicht berücksichtigt.Beispiel einer verketteten Funktion: f(x) = u[v(x)] Nach der Kettenregel gilt also: f ‚(x) = v'(x) × u'[v(x)] Die Funktion f ist also bezüglich der Funktion f ‚ eine Stammfunktion. Die Stammfunktion für g(x) = h'(x) × k[h(x)] lautet deshalb G(x) = K[h(x)] Wenn die Funktion k eine Potenzfunktion der Form k(z) = z – 4 ist Mit z = h(x) = x2 – 3 erhalte ich eine gesuchte Stammfunktion F: F(x) = – 1/3-3 × (x2 – 3) -3 |
Wie bilde ich eine Stammfunktion? |
| Eine Stammfunktion zu bilden wird auch „Aufleiten“ genannt, ergo das Gegenteil vom Ableiten. Eine beliebige, ganzrationale Funktion hat unendlich viele Stammfunktionen. Die nächst höhere Stammfunktion wird wie folgt gebildet.Zunächst ist es so, dass alle Exponenten einer Funktion beim „Aufleiten“ um plus eins größer werden. Die Zahl vor dem x wird hierbei zunächst außer Acht gelassen. Aus einem x wird also ein x^2 (sprich: X Quadrat), aus einem x^2 wird dementsprechend ein x^3 (sprich: X hoch drei), und so weiter. Als nächstes schaut man sich die Zahlen, die vor den Xen stehen, an. Diese werden durch den jeweiligen neuen Exponenten, geteilt. Der y-Achsenabschnitt, welchem bis dahin noch kein x anhängt, wird beim Bilden der Stammfunktion um ein x ergänzt. Existiert kein y-Achsenabschnitt, kann dieser – theoretisch – beliebig gewählt werden, darin begründet sich die unendliche Anzahl an Stammfunktionen. In der Praxis schreibt man dann stellvertretend für den y-Achsenabschnitt „+ a“. |