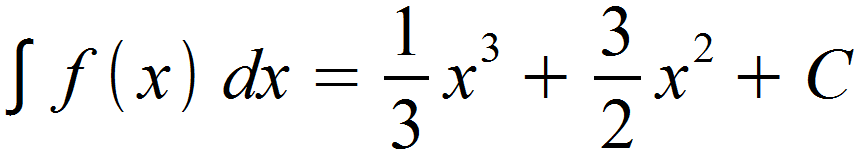Summenregel bei Integration
Besteht eine Funktion f (x) aus mehreren Summanden, so werden diese als einzelne Funktionen betrachtet und können auch einzeln aufgeleitet werden.
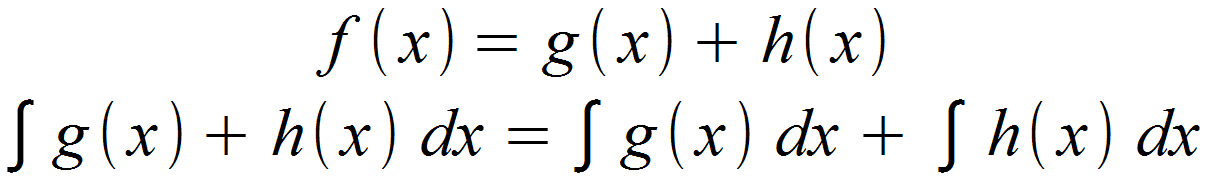
Voraussetzung ist also, dass die Teilfunktionen jeweils durch ein Pluszeichen (oder Minuszeichen) getrennt sind.
Unser Lernvideo zu : Summenregel bei Integration
Beispiel
Die folgende Funktion bestehend aus zwei Termen soll aufgeleitet werden.
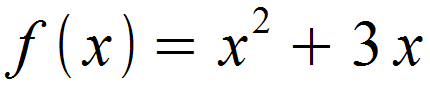
Wir definieren die Terme x2 und 3x als separate Funktionen.
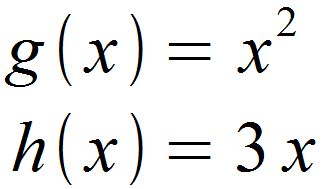
Diese leiten wir nun nach den bekannten Regeln für Potenzen und Faktoren auf.
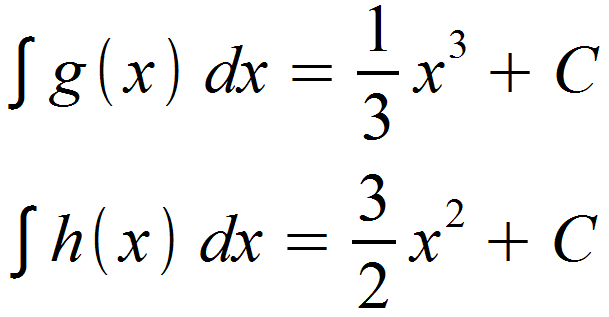
Eingesetzt in die Formel der Summenregel bedeutet dies für die Aufleitung von f (x) abschließend die Addition der integrierten Teilfunktionen. Die Konstanten aus der Integration der Teilfunktionen werden hierbei zu einer neuen Konstante C zusammengefasst. Tauchen die gleichen Potenzen von x mehrmals auf, kann optional noch zusammengefasst werden. Dies ist hier jedoch nicht der Fall und wir erhalten somit: