Partielle Integration
Die partielle Integration wird verwendet, wenn ein Produkt aufgeleitet werden soll, dessen Faktoren jeweils von x abhängig sind. Eine Abhängigkeit von x bedeutet im Grunde einfach, dass die Faktoren irgendwo ein x enthalten. Die Formel lautet wie folgt:
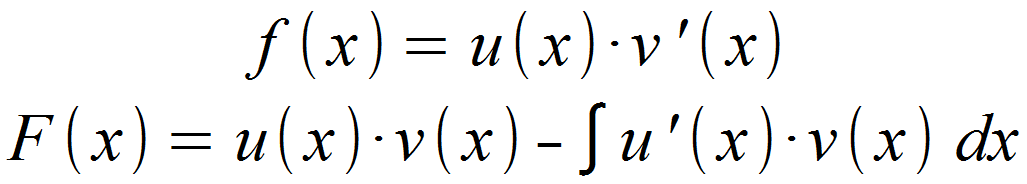
Alternativ lautet die Formel in Integralschreibweise ausgedrückt:
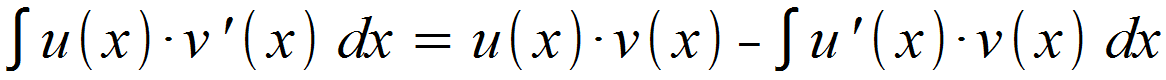
Die partielle Integration kann als Gegenstück zur Produktregel beim Ableiten betrachtet werden und wird daher auch Produktintegration genannt.

Bei der Anwendung ist darauf zu achten, dass die Teilfunktionen u (x) und v ‚(x) möglichst geschickt gewählt werden. Da es sich bei der zu untersuchenden Funktion um ein Produkt handelt, lassen sich dessen Teilfunktionen beliebig definieren, weil sich die Faktoren eines Produkts ja auch beliebig vertauschen lassen. Mit Hinblick auf die Formel ist es sinnvoll u (x) so zu wählen, dass die Ableitung u ‘(x) möglichst simpel wird. Oder anders ausgedrückt die Aufleitung v (x) von v ‚(x) nicht unnötig komplex wird.
Für die Wahl von u (x) kann man sich grob an folgenden Leitfaden halten:
- Logarithmische Funktionen (log, ln…)
- Algebraische Funktionen (x3, 2·x5…a·xn)
- Trigonometrische Funktionen (sin, cos, tan…)
- Exponentialfunktionen (ex)
Unser Lernvideo zu : Partielle Integration
Beispiel
Die folgende Funktion soll abgeleitet werden. Sie ist das Produkt einer Exponentialfunktion (ex) sowie einer algebraischen Funktion (x).
![]()
Im ersten Schritt gilt es u (x) und v ‚(x) sinnvoll zu wählen. Wir wählen anhand des obrigen Leitfadens die Exponentialfunktion für u (x) und dementsprechend die algebraische Funktion für v ‚(x).
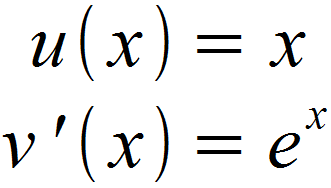
Anschließend leiten wir u (x) ab und integrieren v ‚(x), um u ‚(x) und v (x) zu erhalten.
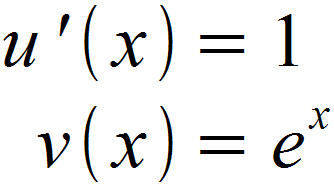
Nun haben wir alle Teilfunktionen, die für die Formel der Stammfunktion benötigt werden. Wir setzen also ein:
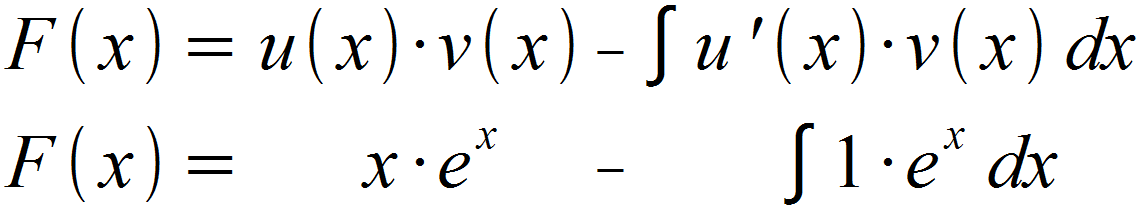
Wir lösen das Integral und können abschließend ex ausklammern.
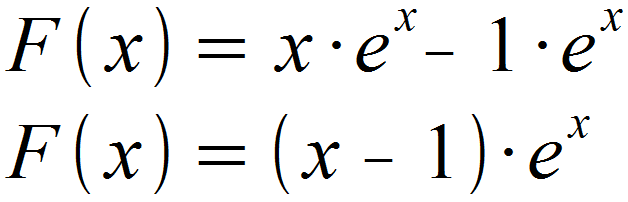
Alternativer Weg
Bei der Wahl der Teilfunktionen kann im Grunde kein Fehler gemacht werden. Die schlechtere Wahl bedeutet lediglich, dass der weitere Rechenweg etwas komplexer wird, was hier verdeutlicht werden soll.
Wir vertauschen also zunächst die Definitionen unserer vorherigen Teilfunktionen u (x) und v ‚(x).
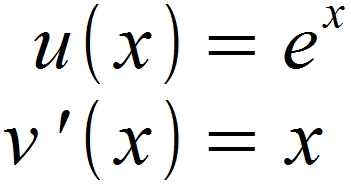
Anschließend leiten wir wieder u (x) ab und integrieren v ‚(x), um u ‚(x) und v (x) zu erhalten.
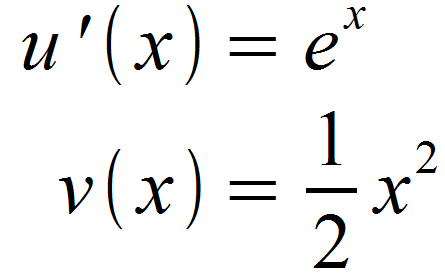
Wir setzen unsere Teilfunktionen wieder in die Formel für die Stammfunktion ein.
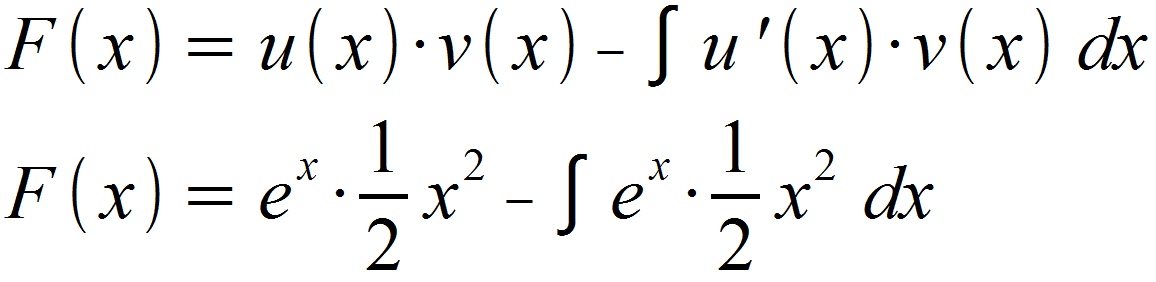
Wie man sieht, müssten wir zum Lösen des Integrals erneut eine partielle Integration durchführen, da wir wieder ein Produkt mit zwei Faktoren vorlieren haben, die beide von x abhängig sind. Wir sparen uns diesen Schritt, da die vorherige Lösung hier der bessere Weg ist. Falls man also erneut auf eine partielle Integration stößt, lohnt es sich oft, zunächst die zweite Möglichkeit zu prüfen.
