Sattelpunkt
Ein Sattelpunkt wird auch Terrassenpunkt oder Horizontalwendepunkt genannt und ist ein kritischer Punkt einer Funktion, der nicht zu den Extrempunkten zu zählen ist. Sattelpunkte sind Wendepunkte mit waagerechter Wendetangente. Demnach müssen folgende drei Bedingungen erfüllt sein:
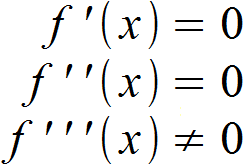
Grafisch kannst du dir den Sattelpunkt folgendermaßen vorstellen, hier anhand der Beispielfunktion f (x) mit der waagerechten Wendetangente t (x) verdeutlicht:
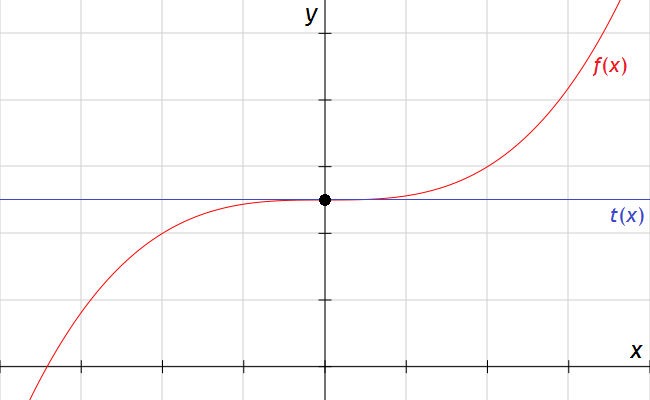
Sollen die Sattelpunkte einer Funktion berechnet werden, verfährt man am besten nach folgendem Schema:
- Erste Ableitung bilden
- Nullstellen der ersten Ableitung berechnen
- falls kein x-Wert für f '(x) = 0 existiert, hier abbrechen
- Zweite Ableitung bilden
- Nullstellen der ersten Ableitung in die zweite Ableitung einsetzen
- falls keiner der x-Werte für f “(x) = 0 ergibt, hier abbrechen
- Dritte Ableitung bilden
- Nullstellen der ersten und zweiten Ableitung in die dritte Ableitung einsetzen
- falls keiner der x-Werte für f “'(x) ≠ 0 ergibt, hier abbrechen
- positive x-Werte in f (x) einsetzen, um y-Koordiaten der Sattelpunkte zu erhalten
Beispiel
Die folgende Funktion soll auf Sattelpunkte untersucht werden.
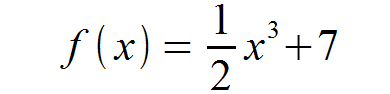
Wir bilden also zunächst die erste Ableitung.
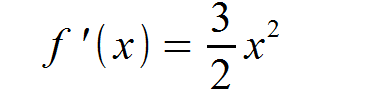
Um die Nullstellen der ersten Ableitung zu berechnen, setzen wir diese gleich Null und lösen nach x auf.
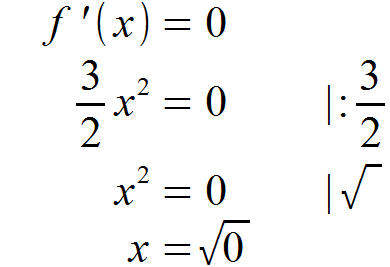
Somit erhalten wir für die Nullstelle folgenden x-Wert:
![]()
Da wir für die erste Ableitung eine Nullstelle erhalten haben, bilden wir im nächsten Schritt die zweite Ableitung.
![]()
Wir setzen unsere Nullstelle in die zweite Ableitung ein und prüfen, ob das Ergebnis f “(x) = 0 ist.
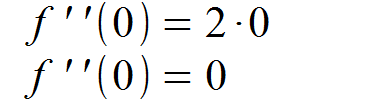
Da die zweite Ableitung für unsere Nullstelle ebenfalls Null ergibt, bilden wir nun die dritte Ableitung.
![]()
Wir setzen unsere Nullstelle in die dritte Ableitung ebenfalls sein.
![]()
Das Ergebnis ist f “(x) ≠ 0 und somit sind all unsere Bedingungen für einen Sattelpunkt erfüllt. Zuletzt bestimmen wir noch den y-Wert unseres Sattelpunkts.
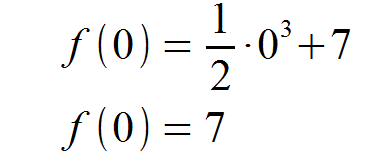
Somit liegt für f (x) abschließend folgender Sattelpunkt vor:
![]()
