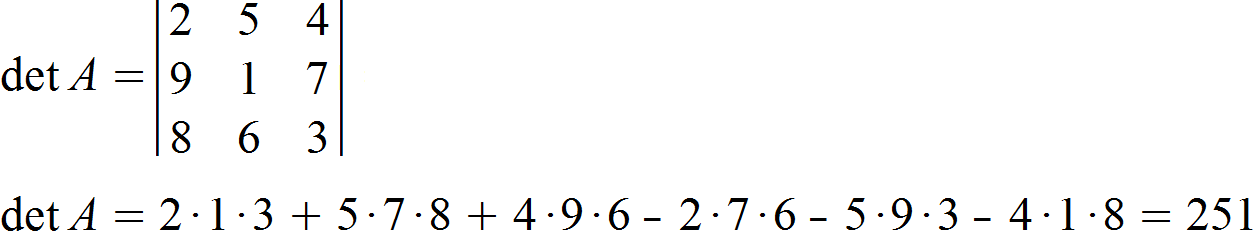Determinante
Die Determinante ist eine eine reelle Zahl, die einer quadratischen Matrix zugeordnet werden kann. Liegt eine quadratische Matrix A vor, so wird deren Determinante als det A bezeichnet.
Wie du schon weißt, werden die Elemente einer Matrix mit runden Klammern umschlossen. Um die Determinante einer Matrix zu kennzeichnen, umschließt man die gleichen Elemente mit geraden Strichen.
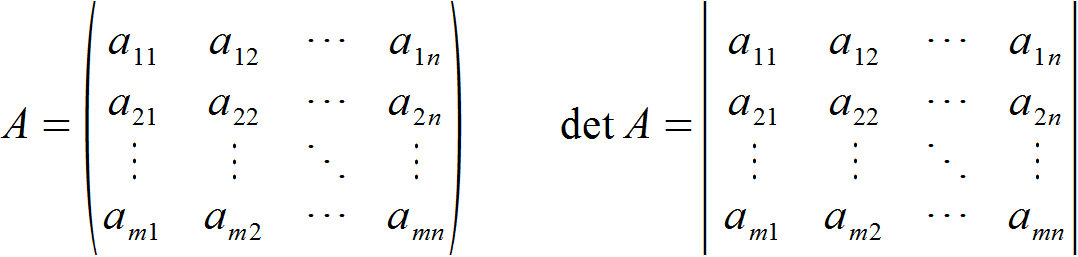
Aber wofür werden Determinanten gebraucht?
Liegt beispielsweise ein lineares Gleichungssystem als Matrix vor und dessen Determinante ist ungleich Null, so ist dieses lineare Gleichungssystem eindeutig lösbar. Das bedeutet anders ausgedrückt, dass jeder Variable des linearen Gleichungssystems ein konkreter Zahlenwert zugeordnet werden kann. Ist die Determinante einer quadratischen Matrix ungleich Null, lässt sich diese zudem invertieren.
![]()
Eine weitere Schreibweise für die Determinante det A der Matrix A ist |A|.
- det A = |A|
Berechnung
Die Bestimmung der Determinanten wird für größere Matrizen schnell sehr komplex, weshalb wir uns hier auf die beiden kleinsten quadratischen Matrizen fokussieren möchten, für die sich die Formeln noch einigermaßen gut behalten lassen.
(2,2)-Matrix
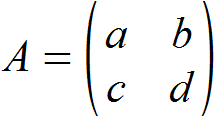
Die Determinante einer (2,2)-Matrix zu bestimmen ist einfach. Wir bilden zunächst das Produkt der Elemente, die sich auf der Diagonalen von oben links nach unten rechts befinden. Davon ziehen wir das Produkt der Elemente ab, die sich auf der Diagonalen von oben rechts nach unten links befinden.
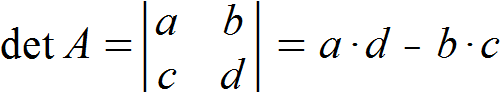
Beispiel
Es soll die Determinante der folgenden (2,2)-Matrix bestimmt werden.
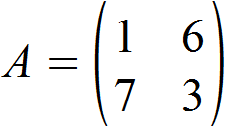
Wir gehen nach der oben genannten Formel vor und erhalten somit für die Determinante:
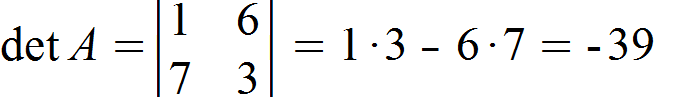
(3,3)-Matrix
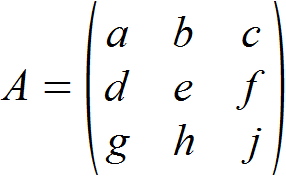
Die Determinante einer (3,3)-Matrix zu bestimmen ist etwas komplizierter, aber auch nicht schwer. Das Prinzip bleibt im Grunde gleich. Wir bilden zunächst die Produkte der Elemente, die sich auf den Diagonalen von oben links nach unten rechts befinden. Da ein Produkt allerdings immer aus jeweils einem Element aller Zeilen bestehen muss, fügen wir die Diagonalen mit zwei Elementen jeweils mit dem Element zusammen, welches sich in der noch nicht abgedeckten Zeile befindet. Davon ziehen wir die Produkte der Elemente ab, die sich auf den Diagonalen von oben rechts nach unten links befinden.
Da der Vorgang in Worten verwirrender klingt als er letztenendes ist, hier die Formel mit Variablen:
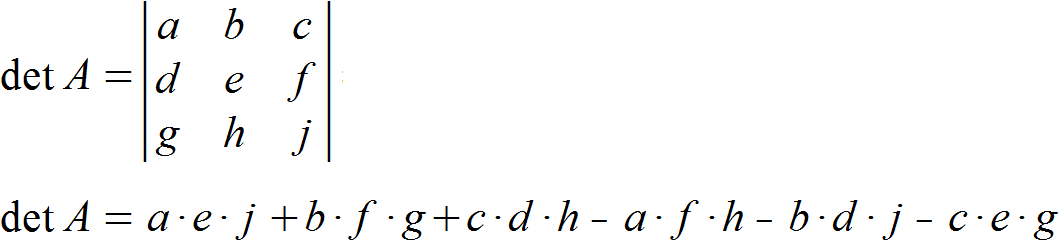
Beispiel
Es soll die Determinante der folgenden (3,3)-Matrix bestimmt werden.
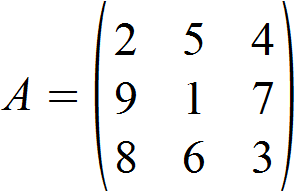
Wir gehen wieder nach unserer Formel vor und erhalten für die gesuchte Determinante: