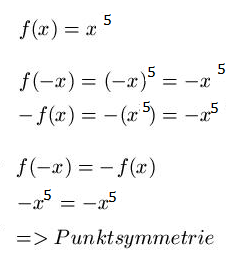Standartsymmetrie
In der Geometrie spielt der Begriff Symmetrie eine wichtige Rolle bei der Betrachtung von eindimensionalen, zweidimensionalen und dreidimensionalen Objekten. Ein Objekt heißt symmetrisch, wenn es durch Bewegungen (z.B. Spiegelung, Drehung oder Verschiebung) auf sich selbst abgebildet werden kann.
Bei einer Punktsymmetrie spiegelt man jeden Punkt an einem Punkt, so dass dann alle Punkte wieder übereinstimmen. Die Punktsymmetrie beschreibt die Symmetrie eines Objekts um einen Punkt herum. Die Punktsymmetrie entspricht einer Drehung der Figur um genau 180 Grad. Somit ist die Punktsymmetrie ein Spezialfall der Drehsymmetrie.
Symmetrie bei Funktionsgraphen
Der Graph einer Funktion kann die Eigenschaft haben symmetrisch zu verlaufen bezüglich einem Objekt, sprich einem Punkt oder einer Geraden. Symmetrisch bedeutet, dass man den Graphen der Funktion teilen kann in zwei „gleiche“ Strecken, die eine entsteht dann durch Spiegelung der anderen am Symmetriepunkt bzw. an der Symmetriegeraden und umgekehrt.
Beispiele für Punktsymmetrie ( Standartsymmetrie)
Bei einem Vierteck liegt Punktsymmetrie (in sich) genau dann vor, wenn es sich um ein Parallelogramm handelt. Das Symmetriezentrum ist dann der Schnittpunkt der Diagonalen. Als Spezialfälle des Parallelogramms sind Rechteck, Raute und Quadrat punktsymmetrisch.
- Jeder Kreis ist (in sich) punktsymmetrisch bezüglich seines Mittelpunkts.
- Zwei Kreise mit gleichem Radius sind zueinander punktsymmetrisch. Das Symmetriezentrum ist der Mittelpunkt der Verbindungsstrecke der beiden Kreismittelpunkte.
- Mehrere Symmetriezentren kann es nur geben, wenn die Figur nicht beschränkt ist. Das einfachste Beispiel ist die Gerade. Sie hat sogar unendlich viele Symmetriezentren.
- Ein Dreieck ist niemals punktsymmetrisch. Es können aber zwei Dreiecke zueinander punktsymmetrisch sein.
Kombination
Es gibt 6 verschiedene Kombinationsmöglichkeiten die du wissen solltest!
Aus der Möglichkeit, Symmetrieoperationen zu kombinieren, lassen sich die symmetrischen Grundoperationen herleiten:
- Identität (Null-Operation, keine Veränderung)
- Rotation (Drehung)
- Rotation – Inversion (Drehspiegelung)
- Translation (Verschiebung)
- Gleitspiegelung
- Schraubung
Ohne zu Rechnen die Symmetrieart bestimmen
Man kann die Symmetrieart auch ohne zu rechnen bestimmen. Der Trick besteht darin, dass du die Exponenten dir genau anguckst.
Merke: Sind im Funktionsterm alle Potenzen von x ungerade, so ist der Graph punktsymmetrisch zum Ursprung
Beispiel
2/3x3-0,8x1 ⇒ Exponent ungerade also Punktsymmetrie
oder
1/3x3-x ⇒Exponent ungerade also Punktsymmetrie
Merke: X ohne Exponent gilt als ungerader Exponent; Bsp x3-2x = x3-2x1
Rechnerisch