Klammer ausmultiplizieren
Wenn ein Term mit einer Klammer, in der eine Summe oder Differenz steht, multipliziert werden soll, muss der Term mit jedem Glied in der Klammer multipliziert werden, um die Klammer aufzulösen
Wenn ein Term
- mit einer Klammer, in der eine Summe oder Differenz steht,
- multipliziert werden soll,
muss
- jeder Summand bzw. Minuend und Subtrahend
- mit diesem Term multipliziert werden,
um die Klammer ganz auszumultiplizieren
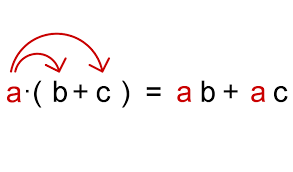
►Jeder aus der ersten Klammer mit jedem aus der zweiten Klammer
Wir schauen uns einige Beispiele an

oder
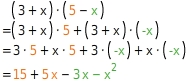
Klammer mal Faktor
- Wie man Klammern auflöst, wissen wir schon, falls wir uns an das Distributivgesetz erinnern. Wir multiplizieren jeden Summanden in der Klammer mit dem Faktor vor der Klammer. Also zum Beispiel:
- 5x – 2 (8x – 2) = 5x – 16x + 4 = – 11x + 4
Klammer mal Klammer
- Wir müssen jeden Summanden aus der ersten Klammer mit jedem Summanden aus der zweiten Klammer multiplizieren. Beispiel:
- (5x – 2) (8x – 2) = 5x · 8x + 5x · (– 2) + (– 2) · 8x + (– 2) · (– 2) = 40x² – 10x – 16x + 4
Plus vor der Klammer
- Wenn in einem Term etwas vorkommt wie 5x + (8x – 2), also Term plus Klammer, dann stellen wir uns einfach vor, dass vor der Klammer der Faktor 1 steht und lösen das auf wie Klammer mal Faktor:
- 5x + (8x – 2) = 5x + 1 · (8x – 2) = 5x + 1 · 8x – 1 · 2 = 5x + 8x – 2
Minus vor der Klammer
- Wenn wir etwas minus einer Klammer rechnen, also sowas wie 5x – (8x – 2), dann stellen wir uns auch in diesem Fall vor, dass vor der Klammer der Faktor 1 steht und rechnen aus wie Faktor mal Klammer:
- 5x – (8x – 2) = 5x – 1 · (8x – 2) = 5x + (– 1) (8x – 2) = 5x + (–1) · 8x + (– 1) (– 2) = 5x – 8x + 2
- Wir stellen fest, dass das Minus praktisch die Vorzeichen umdreht und man im selben Schritt die Klammern weglässt.
Regeln des Rechnens mit negativen Zahlen:
(1) minus auf plus ergibt minus
(2) minus auf minus ergibt plus
Ähnlich wie beim Ausmultiplizieren eines Faktors vor der Klammer folgt das Ausmultiplizieren zweier Klammern diesen Vorzeichenregeln:
- (+)⋅(+)=(+)
- (+)⋅(−)=(−)
- (−)⋅(+)=(−)
- (−)⋅(−)=(+)
Beim Ausmultiplizieren geht es um den Distributivgesetz. Diese sollte man sehr gut beherrschen, um später Fehler zu vermeiden. das Distributivgesetz lautet
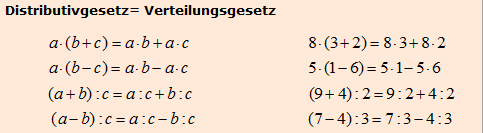
Aber auch die anderen Gesetze sollte man gut beherrschen und Anwenden können. Neben des Distributivgesetzes gibt es noch 2 andere. Diese lauten

