Zahlenmengen
In der Mathematik gibt es verschiedene Zahlenbereiche. Wir möchten hier die wichtigsten Zahlenbereiche vorstellen.
Unser Lernvideo zu : Zahlenmengen
Natürliche Zahlen
Als Erstes lernt man in der Schule mit den natürlichen Zahlen umzugehen. Die natürlichen Zahlen sind die Zahlen, die beim Zählen verwendet werden: 1, 2, 3, 4, 5, 6, und so weiter. Als Symbol verwenden wir ![]() . Ein N mit einem Doppelstrich. Der Doppelstrich kommt übrigens bei allen Symbolen für Zahlenbereiche vor.
. Ein N mit einem Doppelstrich. Der Doppelstrich kommt übrigens bei allen Symbolen für Zahlenbereiche vor.
Mathematisch korrekt können wir die Definition der natürlichen Zahlen so schreiben:
![]() = {1; 2; 3; 4; 5…}
= {1; 2; 3; 4; 5…}
Die Null gehörte ursprünglich nicht zu den natürlich Zahlen. Heute wird sie aber häufig zu den natürlichen Zahlen dazugezählt.
Natürliche Zahlen sind also alle ganzen Zahlen (Zahlen ohne Komma) die positiv sind. Wichtig zu wissen ist, dass es keine höchste natürliche Zahl gibt. Egal welche Zahl man sich vorstellt, es gibt immer noch eine größere. Es gibt also unendliche viele natürliche Zahlen.
Ganze Zahlen
Als nächstes lernt man meistens die ganzen Zahlen kennen. Dies sind alle Zahlen die keine Nachkommastellen haben. Sie dürfen allerdings negativ sein. Abgekürzt werden sie mit einem ![]() , welches einfach für Zahlen steht. Auch hier begegnet und wieder der Doppelstrich in der Mitte vom Z.
, welches einfach für Zahlen steht. Auch hier begegnet und wieder der Doppelstrich in der Mitte vom Z.
![]() = {…, -5, -4, -3, -2, -1 ,0, 1, 2, 3, 4, 5, …}
= {…, -5, -4, -3, -2, -1 ,0, 1, 2, 3, 4, 5, …}
Die ganzen Zahlen umfassen also alle negativen und positiven Zahlen, die keine Nachkommastellen besitzen.
Rationale Zahlen
Die nächste Menge die man kennenlernt ist die der rationalen Zahlen. Diese Zahlenenge umfasst neben den ganzen Zahlen auch fast alle Kommazahlen. Allgemein gesprochen sind alle Zahlen rational, die als Bruch zweier ganzer Zahlen dargestellt werden können. Das Zeichen für die rationalen Zahlen ist das ![]() .
.
Einige Beispiele für rationale Zahlen sind:
![]()
Es gehören jedoch nicht alle Zahlen zu den rationalen Zahlen. Im nächsten Abschnitt (Irrationale Zahlen) wird erklärt, welche nicht dazu gehören.
Irrationale Zahlen
Irrationale Zahlen sind alle Zahlen, die nicht zu der Menge der rationalen Zahlen gehören. Beispiele für solche Zahlen sind:

Dies sind bekannte Zahlen, die in der Mathematik oft benötigt werden. Das besondere an irrationalen Zahlen ist, das sie sich nicht durch einen Bruch ganzer Zahlen ausdrücken lassen. Sie können auch nicht als Periode geschrieben werden, da sie keine derartige Regelmäßigkeit aufweisen.
Man kann diese Zahlen also nicht exakt darstellen, da sie theoretisch unendlich viele Nachkommastellen haben. Ein allgemeines Symbol für die irrationalen Zahlen gibt es nicht.
Reelle Zahlen
Die übergeordnete Menge der hier vorgestellten Zahlenbereiche sind die reellen Zahlen. Sie umfassen die natürlichen Zahlen, die ganzen Zahlen, die rationalen Zahlen und die irrationalen Zahlen. Das Symbol für die reellen Zahlen ist das ![]() .
.
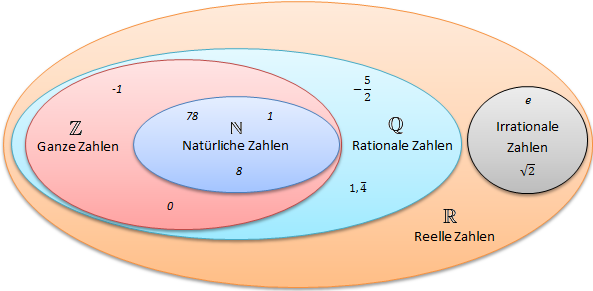
Zahlenmengen im Überblick
In diesem Mengendiagramm können wir die Zusammenhänge sehr gut erkennen:
- Alle natürlichen Zahlen sind Ganze Zahlen
- Alle ganzen Zahlen sind rationale Zahlen
- Alle rationalen Zahlen sind reelle Zahlen
- Alle irrationalen Zahlen sind reelle Zahlen
- Die Menge der rationalen Zahlen und die Menge der irrationalen Zahlen bilden die Menge der reellen Zahlen