Dezimalbruchentwicklung

Dezimalbruchentwicklung

Was ist eigentlich Dezimalbruchentwicklung?

• Dezimalbruchentwicklung ist nichts anderes als periodische Dezimalzahlen in Brüche umformen! In der Mathematik wird es folgendermaßen definiert

Diese Anwendung dieser Formel soll anhand eines Beispiels erklärt werden:

p=048363636…

x=48

m=2

y=36

n=2

⇒

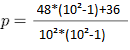
⇒Dabei sind p die periodische Zahl, x die Zahl vor Beginn der Periode (als Ganzzahl), m die Anzahl der Ziffern vor Beginn der Periode, y die Ziffernfolge der Periode (als Ganzzahl) und n die Länge der Periode.

Was ist eine periodische Dezimalzahl?

• Eine periodische Dezimalzahl erkennst du daran, dass sich eine Ziffer oder eine Folge von Ziffern nach dem Komma immer wiederholt. Die Wiederholungen können bei der ersten Nachkommastelle beginnen, sie können aber auch erst später beginnen.
• Beispiel siehe unten!

Periode

• Die Periode eines Bruchs mit dem Nenner n kann höchstens n-1 Stellen haben, denn spätestens beim n-ten Rest muss sich ein bereits dagewesener Rest wiederholen.

Arten der Dezimalbruchentwicklungen

• gemischtperiodische
• reinperiodische
• abbrechende ( endliche)

Arten der Dezimalbruchentwicklung mit jeweiligem Beispiel

gemischtperiodische :sind Dezimalzahlen, bei denen zwischen der Periode und dem Komma noch mindestens eine Ziffer steht. Der gekürzte Bruch mit Zähler m und Nenner n > 1 besitzt genau dann eine gemischt periodische Dezimalbruchentwicklung, wenn der Nenner n den Primfaktor 2 oder den Primfaktor 5 und darüber hinaus mindestens einen weiteren, von 2 und 5 verschiedenen, Primfaktor hat.

0,16666… =0.16¯

12.34121,212…=12.3412¯

reinperiodische: sind Dezimalzahlen, bei denen die Periode direkt nach dem Komma beginnt. Der gekürzte Bruch mit Zähler m und Nenner n > 1 besitzt genau dann eine rein periodische Dezimalbruchentwicklung, wenn der Nenner n weder den Primfaktor 2 noch den Primfaktor 5 hat.

 

14,1111….=14,1

0,294294294…=0,294

abbrechend:  Sobald der Rest 0 erstmalig auftritt, endet der Divisionsalgorithmus. Alle nachfolgenden Zifferns sind 0, die Dezimalbruchentwicklung bricht ab. Der gekürzte Bruch mit Zähler m und Nenner n > 1 besitzt genau dann eine endliche Dezimalbruchentwicklung, wenn der Nenner n nur die Primfaktoren 2 und 5 hat.

1/2= 0,5

1/8=0,125

1/50= 0,02

Unser Lernvideo zu : Dezimalbruchentwicklung

---

---

Merke Dir folgendes: 

• Alle Brüche, deren Nenner eine Potenz von 10 (1, 10, 100, 1000, …) ist, haben keine Periode.
• Nur Brüche, deren Nenner (im vollständig gekürzten Zustand) keine anderen Primfaktoren als 2en und/oder 5en besitzen, ergeben einen unperiodischen Dezimalbruch, der eine endliche Zahl an Kommastellen besitzt.
• Wenn die Dezimalbruchentwicklung nicht abbricht, wird sie irgendwann einmal periodisch.
• Die Dezimaldarstellung einer rationalen Zahl z/n ist entweder abbrechend oder periodisch. Die Periode ist höchstens von der Länge n – 1.
• Jede abbrechende oder periodische Dezimalzahl lässt sich als gewöhnlicher Bruch darstellen, ist also eine rationale Zahl.
• Nur wenn die Faktoren 2 und 5 sind, sind sie endlich,
• nur wenn die Faktoren 2,5 und 10⋅n−1 sind, sind sie reinperiodisch.
• Wenn andere Faktoren reinspielen, sind sie gemischtperiodisch.
• am nenner, wenn unter dem bruchstrich 2, 4, 5, 8, 10, 12 steht, ist er abbrechend, bei 3, 6, 7, 9 und 11 periodisch, höhere zahlen unter dem nenner sind eher selten