Umfang eines Kreises
Wir betrachten hier einen Kreis und erlernen, wie der Umfang des Kreises berechnet wird. Dieser wird auch als Kreisumfang bezeichnet. Dazu schauen wir uns den allgemeinen Kreis noch einmal an.
Zur Wiederholung
Der Kreis ist eine geometrische Figur in der Ebene. Er definiert sich durch die Menge aller Punkte die einen bestimmten Abstand zu einem vorgegebenen Punkt haben. Anders gesagt, ist ein Kreis um einen Mittelpunkt definiert und hat überall den selben Abstand zum Mittelpunkt. Dieer Abstand heißt Radius. Das doppelte des Radius, ist der Durchmesser. Der Durchmesser verläuft durch den Mittelpunkt von Kreislinie zu Kreislinie.
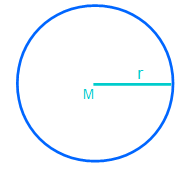
Die Abbildung zeigt einen Kreis. Zu sehen ist auch der Mittelpunkt M um den sich mit dem selben Abstand die Menge aller Punkte den Kreis bilden. Der Abstand vom Mittelpunkt M zum Kreis ist der Radius.
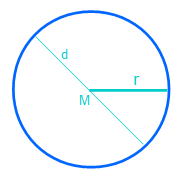
In der zweiten Abbildung ist zusätzlich zum Mittelpunkt M und dem Radius r der Durchmesser d eingezeichnet. Der Durchmesser d ist doppelt so lang wie der Radius r und verläuft durch den Mittelpunkt M.
Wie du ganz einfach den Kreisumfang berechnest?
Normalerweise lernst du in der 8. Klasse im Matheunterricht, wie du ganz einfach den Umfang der Kreise berechnen kannst. Hier kommen wir auf die Kreiszahl Pi zu sprechen ebenso wie auf die Umfangsformen. Je nachdem, welche der Angaben gegeben ist, ergeben sich unterschiedliche Formeln.
Gerade die Kreisberechnung bereitet Kopfzerbrechen. Dabei gibt es im Tafelwerk eben genau die richtigen Formeln, zur Berechnung der Größen.
Zunächst einmal eine gute Nachricht, die Kreise sind zumindest ähnlich gebaut. So bleibt auch das Verhältnis des Kreisdurchmessers und des Kreisumfangs recht konstant. Aus diesem Grund hat sich die Konstante Kreiszahl Pi = 3,14159 … als Zahlenwert für das Verhältnis durchgesetzt. Wir ordnen diese Zahl den transzendenten Zahlen zu, die im Allgemeinen der Mathematik eine höhere Bedeutung haben. So findest du Pi auch auf deinem Taschenrechner.
Die folgenden Kreisgrößen können wir mithilfe dieser Zahl berechnen:
- Kreiszahl
- Umfang
- Kreisfläche
- Krümmung
- Durchmesser
- Kreisbogen
- Kreissektor
- Kreissehne
Wer mit diesem Themenkomplex grundlegende Verständnisschwierigkeiten hat, sollte sich zunächst einmal mit den geometrischen Einheiten des Kreises eingehend befassen. So werdet ihr auf der Stelle treten, wenn ihr nicht wisst, was mit den Kreisflächen, der Tangente oder dem Bogen gemeint ist und wie sich Kreise geometrisch darstellen lassen.
Lerntool zu Umfang eines Kreises
Unser Lernvideo zu : Umfang eines Kreises
Die Formel des Umfangs
Die Formel des Umfangs eines Kreises ergibt sich nicht wie bei den Vierecken durch Addition der Seitenlängen. Sondern wir brauchen die Kreiszahl Pi  . Mehr zu Pi erfährst du auch auf dieser Homepage unter dem Begriff Kreiszahl.
. Mehr zu Pi erfährst du auch auf dieser Homepage unter dem Begriff Kreiszahl.
Der Umfang ist abhängig vom Radius r. Wir berechnen zweimal den Radius r mal Pi.
![]()
Da wir zweimal den Radius r auch als Durchmesser d bestimmen können, gilt auch die Formel:
![]()
Beide Formel berechnen den Umfang des Kreises und wir können sie nutzen.
Beispiel 1
Wir üben die Berechnung des Kreisumfangs
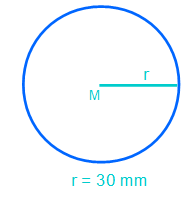
Die Skizze zeigt einen Kreis mit dem Radius 30mm. Wir nutzen die Formel zur Berechnung des Umfangs.
Gegeben: r= 30 mm
Gesucht: U
Formel: U = 2r • 
Einstzen und berechnen: U = 2 • 30mm •  = 60mm •
= 60mm •  = 188,4mm
= 188,4mm
Antwort: Der Umfang des Kreises ist 188,4mm.
Beispiel 2
Nun betrachten wir einen Kreis dessen Umfang wir bereits kennen.
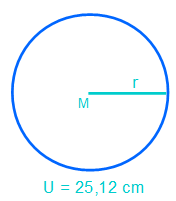
Bei diesem Beispiel ist der Umfang angegeben, so dass wir nun den Radius r errechnen wollen. Dazu stellen wir zunächst die Formel nach r um:
U = 2 r  | :2
| :2 
U: (2 ) = r
) = r
Nun können wir den gesuchten Radius r berechnen.
Gegeben: U = 25,12cm und 
Gesucht: r
Einsetzen und berechnen: r = 25,12cm : (2  ) = 12,56cm :
) = 12,56cm :  = 4cm
= 4cm
Antwort: Der Radius r ist 4 cm lang.
