Spezielle Vierecke
Neben den allgemein bekannten Vierecken gibt es noch viele weitere Vierecke mit Besonderheiten, die wir euch hier vorstellen wollen. Auch bei diesen Vierecken sind natürlich 4 Ecken und für Kanten gegeben. Auch hier ist die Innenwinkelsumme 360°.
Das Sehnenviereck
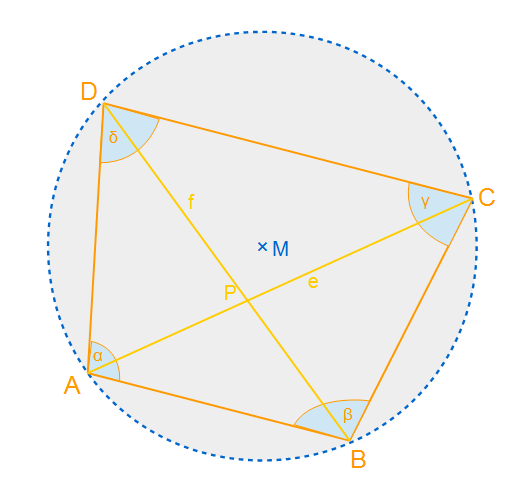
Das Sehnenviereck ist ein Viereck, dessen Eckpunkte alle auf einem Kreis liegen. Der Kreis ist der Umkreis des Vierecks. Alle Punkte sind gleich weit vom Mittelpunkt M entfernt und haben die Strecke des Radius. Die gegenüberliegende Winkel ergeben addiert immer 180°. Dies ergibt sich aus dem Kreiswinkelsatz, den ihr auch auf mathe-lerntipps.de finden könnt.
Das Tangentenviereck
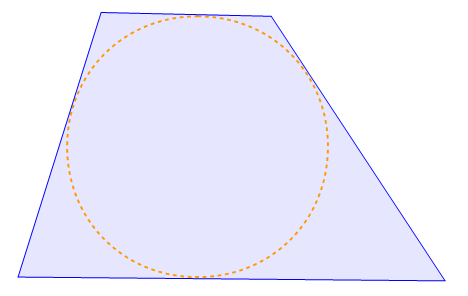
Bei einem Tangentenvierecks sind die Seiten des Vierecks die Tangenten eines Kreises. Somit ist der Kreis der Innenkreis des Vierecks. Die Summe zweier gegenüberliegende Winkel ist identisch mit der Summe der beiden anderen gegenüberliegende Winkel, somit gilt: α + β = γ + δ. Die Winkelhalbierenden schneiden sich in einem Punkt, der auch der Mittelpunkt des Inkreises ist.
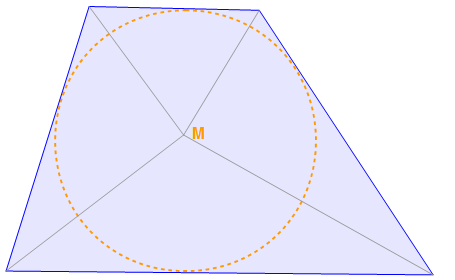
In der Abbildung seht ihr die Winkelhalbierende des Vierecks und sie Treffen sich in einem Punkt. Dieser Punkt ist auch der Mittelpunkt des Kreises.
Unser Lernvideo zu : Spezielle Vierecke
Das konkave Viereck
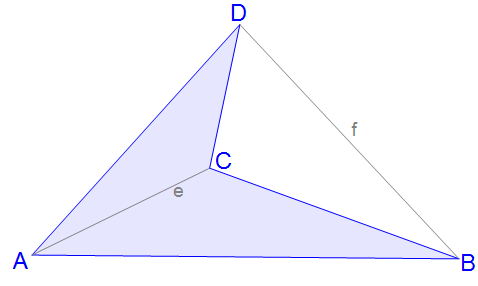
Das konkave Viereck hat wie alle Vierecke vier Eckpunkte und vier Kanten. Auch sind zwei Diagonale im Viereck vorhanden, die die Punkte A und C und die Punkte B und D verbinden. Bei einem konkavem Viereck liegt eine der Diagonalen außerhalb des Vierecks.
Das überschlagene Viereck
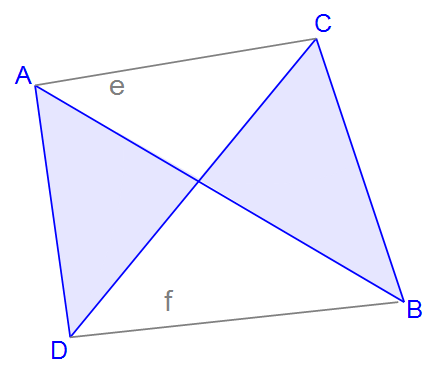
Das überschlagene Viereck ist im Grunde in sich gedreht. Es gibt vier Eckpunkte und vier Seiten. Die beiden Diagonalen liegen außerhalb des Vierecks.
