Symmetrie von Vierecken
Wie wir bereits auf unserer Homepage erwähnt haben, gibt es in geometrischen Figuen oft eine sogenannte Symmetrie. Eine Symmetrie besteht bei einer geometrischen Figur dann, wenn man durch eine Bewegung die Figur auf sich selbst abbilden kann. In der ebenen Geometrie gibt es Achsensymmetrie und Punktsymmetrie.
Eine Symmetrieachse ist eine gerade Linie durch einen bestimmten Punkt in einer Figur. An einer Symmetrieachse kann man die Figur spiegeln.
Bei einer Punktsymmetrie, gibt es einen bestimmten Punkt in der geometrischen Figur, an dem man die Figur um eine bestimmte Gradzahl drehen kann und sie bildet sich wieder auf sich selbst ab.
Auch in Vierecken kann man Symmetrieachsen oder Symmetriepunkte finden. Dieses ist jedoch nicht in jedem Viereck möglich. Einige Vierecke haben keinerlei Symmetrie wie z.B. ein konkaves Viereck keine Symmetrie aufweist.
Unser Lernvideo zu : Symmetrie von Vierecken
Drache
In der geometrischen Figur des Drachen gibt es eine Symmetrieachse. Dies ist eine Diagnole.
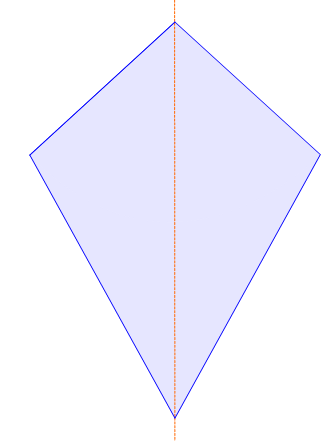
Hier sehen wir einen Drachen, der eine gestrichelte orange Diagonale eingezeichnet hat. Diese Diagonale ist die Symmetrieachse des Drachens. Umgekehrt kann man sagen, wenn nur eine Diagonale eine Symmetrieachse ist, haben wir die Figur des Drachens vor uns.
Raute
Auch die Raute hat Symmetrieachsen. In dieser Figut sind beide Diagonalen des Vierecks auch Symmetrieachsen.
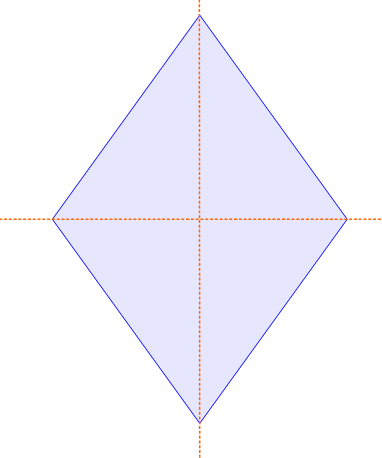
Die abgebildete Raute hat ihre zwei Symmetrieachsen in den beiden Diagonalen. Wenn man die Figur an einer der beiden Achsen spiegelt, bildet sich sich genau auf sich selbst ab.
Gleichschenkliges Trapez
Ein gleichschenkliges Trapez hat zwei parallele Seiten, die aber nicht gleich lang sind und zwei Schenkel, die gleich lang sind. Bei dieser Figur ist die Mittelsenkrechte einer der beiden Parallelen die Symmetrieachse der Figur.
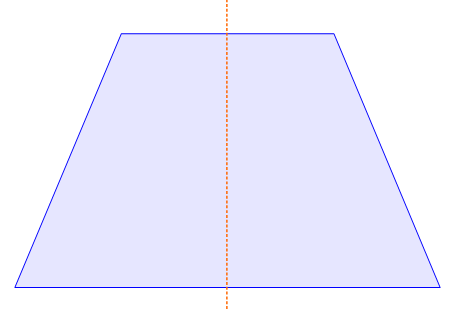
In der Abbildung sehen wir ein gleichschenkliges Trapez. Die Mittelsenkrechte der Parallelen ist auch die Symmetrieachse.
Rechteck
Die Figur des Rechtecks hat zwei Paare von gleichlangen und parallelen Seiten. Die Mittelsenkrechten der Figur sind die Symmetrieachsen in der Figur.
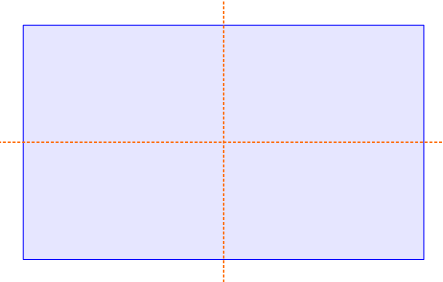
Das Rechteck hat zwei Symmetrieachsen. Dieses sind die Mittelsenkrechten der Seiten. An dem Schnittpunkt der beiden Geraden liegt auch ein Symmetriepunkt. Dreht man das Rechteck an diesem Punkt um 180°, liegt es wieder auf sich selbst auf.
Parallelogramm
Anders als bei den bisher beschriebenen Figuren hat das Parallelogramm keine Symmetrieachsen, sondern nur eine Punktsymmtrie. Dieser liegt in der Mitte des Parallelogramms. Dreht man das Viereck an diesem Punkt um genau 180°, bildet es sich auf sich selbst ab.
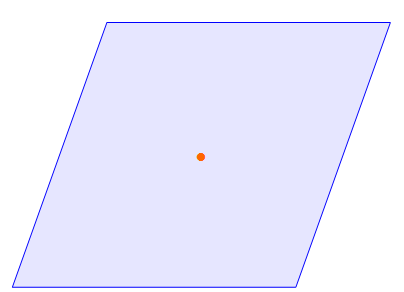
In dieser Abbildung sieht man ein Parallelogramm. An dem orangen Punkt liegt der Symmetriepunkt des Vierecks. Eine Drehung um 180° bringt die Figur wieder auf sich selbst zurück. Dies nennt man zweizählige Punktsymmetrie. Nun ist auch jedes Rechteck eine Parallelogramm. Somit hat auch jedes Rechteck in der Mitte einen Symmetriepunkt.
Quadrat
Das Quadrat hat sowohl Symmetrieachsen als auch einen Symmetriepunkt.
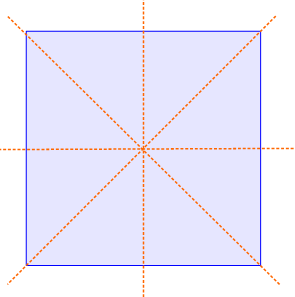
In der Abbildung sehen wie die Symmetrieachsen eines Quadrats. Jedes Quadrat hat vier Symmetrieachsen. Sowohl die beiden Diagonalen als auch die beiden Mittelsenkrechten sind Symmetrieachsen.
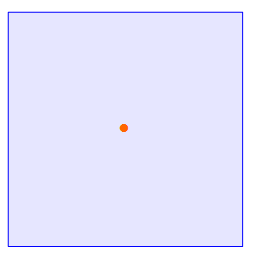
In der Abbildung sie man den Symmetriepunkt des Quadrats. Dreht man das Quadrat an dieser Stelle um 90°, 180° oder 270° gelangt es wieder auf sich selbst zurück. Dieses ist eine sogenannte vierzählige Punktsymmetrie.
