Steigung berechnen

Steigung bestimmen

Wenn wir von einer gezeichneten linearen Funktion die Steigung bestimmen wollen, suchen wir uns am besten zwei Punkte, die wir gut ablesen können und die nicht zu dicht zusammen liegen. Hier ein Beispiel:

 

 

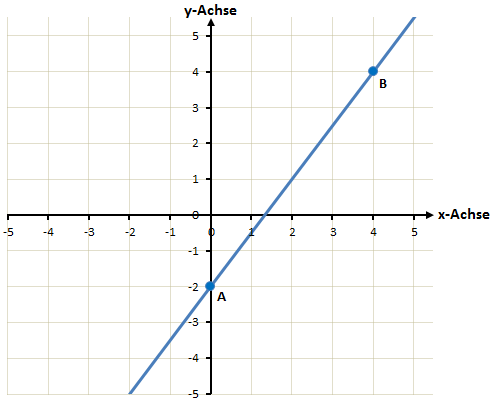
Wir wollen von dieser linearen Funktion die Steigung bestimmen. Wir suchen uns dafür zwei Punkte die wir gut ablesen können. Die beiden gewählten Punkte sind in der Grafik markiert. Um die Steigung zu bestimmen müssen wir nun die x- und y-Differenz der Beiden Punkte bestimmen. Wir notieren also zunächst einmal beide Punkte:

Anschließend berechnen wir die x- und y-Differenz. Wir können dieses grafisch oder rechnerisch machen. Man bezeichnet die Differenz auch als Δ (Delta). Man muss also Δx und Δy bestimmen.

 

 

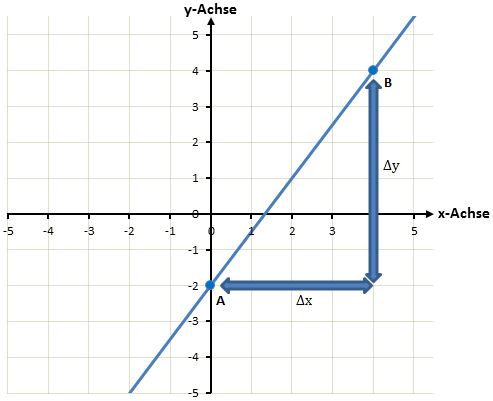
Wir zeichnen ein Steigungsdreieck und bezeichnen die senkrechte Strecke mit Δy (da diese parallel zur y-Achse verläuft) und die waagerechte mit Δx (da diese parallel zu x-Achse verläuft).

Um Δy zu bestimmen brauchen wir also die y-Koordinaten der beiden Punkte A und B. Diese sind 4 und -2. Die Differenz dieser beiden Punkte ist also 4 – (-2) = 6. Δy ist also gleich 6.

Bei Δx ist das Vorgehen das Gleiche. Die beiden x-Koordinaten sind 4 und 0. Die Differenz oder der Abstand der beiden Punkte ist also 4. Δx ist gleich 4.

Wir hätten die beiden Werte auch rein grafisch bestimmen können. Dann hätten wir einfach die Längen der senkrechten und waagerechten Strecke des Steigungsdreiecks im Koordinatensystem ablesen können. Auch dann wären wir auf Δx = 4 und Δy = 6 gekommen.

Um aus diesen beiden Werten nun die Steigung zu bestimmen benötigen wir folgende Formel:

Wir teilen also Δy durch Δx und erhalten die Steigung a:

Die Steigung dieser linearen Funktion ist also a = 1,5.

Das Ergebnis wäre übrigens dasselbe gewesen, auch wenn wir die Punkte A und B vertauscht hätten.

 

Berechnung Steigung bei negativen Steigungen

Eigentlich funktioniert das Ganze bei negativen Steigungen genauso, trotzdem möchten wir es noch einmal an einem Beispiel verdeutlichen.

 

 

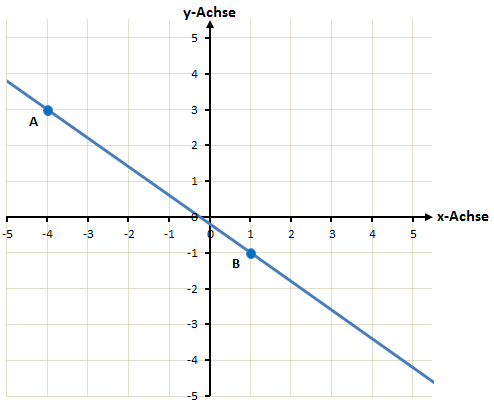
Wir möchten von dieser Funktion die Steigung ermitteln. Wieder suchen wir uns zunächst zwei Punkte die wir gut ablesen können. In diesem Beispiel sind das die beiden Punkte A und B:

Als nächstes zeichnen wir das Steigungsdreieck:

 

 

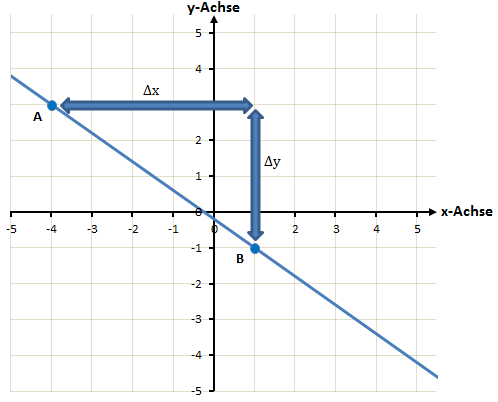
Damit können nun Δx und Δy bestimmt werden:

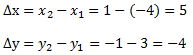
Nun können wir die Steigung bestimmen:

Die Steigung ist also a = -0,8.