Abstand von Punkt zu Ebene
Die einfachste Methode zur Bestimmung des Abstands eines Punkts zu einer Ebene lässt dich dann durchführen, wenn die Ebene in Koordinatenform vorliegt. Falls die gegeben Ebene in einer anderen Form vorliegt, findest du für die Umrechnung in den vorangegangenen Artikeln Hilfe.
![]()
Aus der Koordinatenform lässt sich der Normalvektor der Ebene nämlich direkt entnehmen. Er lautet:
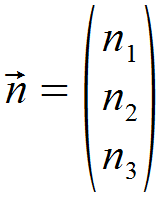
Für die Formel zur Abstandsberechnung benötigen wir die Länge des Normalvektors, welche wir mittels des Betrags folgendermaßen bestimmen:
![]()
Die Formel für die Berechnung des Abstands eines Punkts P ( x | y | z ) lautet dann:
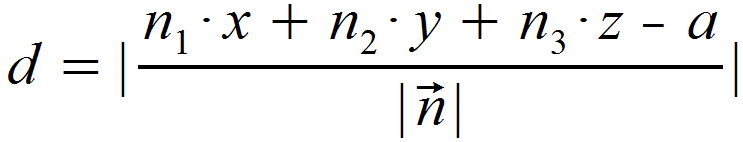

Da wir für den Abstand nur positive Werte erhalten dürfen, müssen wir in der Formel den Betrag vom Bruch nehmen. Oft wird bei Fehlen der Einheit noch LE (für Längeneinheit) an den berrechneten Wert gefügt.
Beispiel
Gegeben sei die Ebene E: 2 x – 11 y + 5 z = 8 und der Punkt P ( 1 | 5 | 6 ). Es soll der Abstand zwischen ihnen berechnet werden.
Lösung
Mit Hinblick auf die Formel für den Abstand entnehmen wir unserer Ebenengleichung in Korrdinatenform zunächst den Normalvektor.
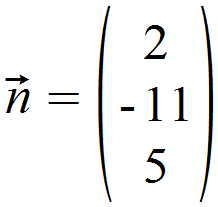
Von dem Normalvektor nehmen wir daraufhin den Betrag.
![]()
Nun haben wir also bereits den Nenner unserer Formel für die Abstandsbestimmung. Für den Nenner formen wir unsere Ebenengleichung in Korrdinatenform so um, dass auf der rechten Seite nur noch Null übrigbleibt.
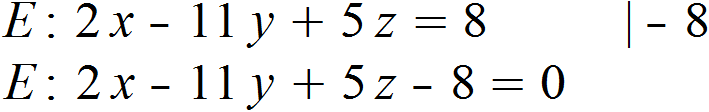
Wir setzen den Punkt P noch in die umgeformte Ebenengleichung ein und erhalten für den Abstand:
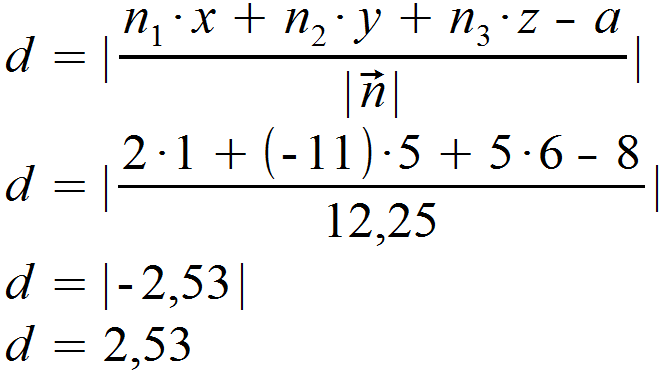
Der Abstand zwischen dem Punkt P und der Ebene E beträgt also d = 2,53 LE.
