Addition Ganzer Zahlen
Wir betrachten nun, wie wir mit Ganzen Zahlen rechnen können. Das Besondere dabei sind natürlich die negativen Zahlen. Diese werden durch ihr Vorzeichen gekennzeichnet und nehmen eine wichtige Rolle ein. Sobald man sich allerdings daran gewöhnt hat, ist das gar kein Problem mehr!
Zahlenstrahl

Wir sehen unseren Zahlenstrahl. Er verläuft von links nach rechts. Wir sehen hier einen Ausschnitt von -9 bis 9. Der Pfeil zeigt an, dass der Strahl nach rechts weiter geht, aber auch dass links noch mehr Zahlen sind als bis -9. Die negativen Zahlen werden oft als rote Zahlen bezeichnet, daher haben wir sie hier auch rot eingesetzt.
Die Null ist als Ursprung zu bezeichnen. Von ihr aus laufen die Zahlenwerte in die beiden Richtungen, einmal ins Positive einmal ins Negative. Jede Zahl hat zu ihrem Nachbarn den selben Abstand. Somit können wir folgern, dass eine bestimmte Zahl sowohl im positiven als auch im negativen Bereich denselben Abstand zur Null hat. Diese Gegebenheit machen wir uns beim Rechnen zu Nutze!
Beim Rechnen mit der Zahlenmenge der Ganzen Zahlen, kann man sich dieses am einfachsten mit einem Bankkonto klarmachen. Wenn man mehr aus gibt als man aktuell auf dem Konto hat, landet man im Negativen Bereich. Bezahlt man dann wieder aufs Konto ein, kommt man aus dem negativen Bereich wieder ins Positive.
Lerntool zu Addition Ganzer Zahlen
Unser Lernvideo zu : Addition Ganzer Zahlen
Addition
Zunächst betrachten wir die Addition an einigen Beispielen. Dabei nutzen wir den Zahlenstrahl, um es auch bildlich zu demonstrieren. Addition der natürlichen Zahlen haben wir bereits in einem vorherigen Kapitel betrachtet. Dies könnt ihr euch natürlich gerne nocheinmal anschauen.
Bei der Addition gilt das Kommutativgesetz, also dass man die Summanden vertauschen kann. Auch bei den Ganzen Zahlen bleibt das Gesetz bestehen. Wir beginnen allerdings immer mit dem ersten Summanden, um das Prinzip ohne zu viel Veränderungen darzustellen.
Beispiel 1:
Berechnen von (-3) + 8
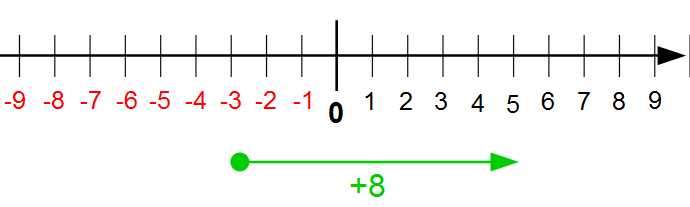
Wir sehen zunächst unseren Zahlenstrahl. Darunter einen neuen grünen Pfeil, dieser beginnt bei -3 und reicht acht Einheiten in die positive Richtung nach rechts und endet bei +5. die Addition von Acht gleicht zunächst das „Minuskonto“ von -3 aus bis Null und dann noch die restlichen 5 Einheiten in die positive Zahlenmenge.
Ergebnis: (-3) + 8 = 5
Beispiel 2:
Berechnen von (-7) + 9
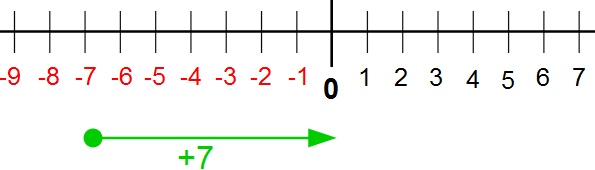
Hier startet der grüne Pfeil bei -7 und geht sieben Einheiten nach rechts in Richtung Positiv, da wir addieren. Sieben Einheiten nach rechts bedeutet, dass er genau bei Null endet.
Ergebnis: (-7) + 7 = 0
Beispiel 3:
Berechnen von (-4) + 2
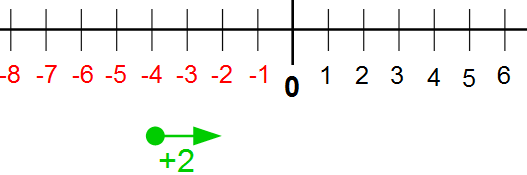
Der grüne Pfeil startet bei -4 und recht zwei Einheiten nach rechts ins die positive Richtung, da wir Addieren und endet bei -2. Da wir auf unserem „Minuskonto“ -4 haben, allerdings nur 2 dazu zählen, erreichen wir nicht die Null oder den positiven Bereich. Dazu bräuchten wir mindestens +4.
Ergebnis: -(4) + 2 = -2
Zusammenfassung
An unseren Beispielen sehen wir, dass wir die negativen ganzen Zahlen genauso behandeln wie die positiven ganzen Zahlen. Alle Zahlen haben den selben Abstand zum Nachbarn, was jeweils eine Einheit ist. Die Null ist der Ursprung oder Scheidepunkt der beiden Bereiche und diesen nutzen wir als Basis um von einem Bereich in den nächsten zu rechnen. Bei der Addition achten wir darauf, dass wir von links nach rechts wandern.
Es ist hilfreich, wenn man im Hinterkopf das Systems eines Bankkontos behält. Auch hier kann man mal im positiven und mal im negativen Bereich sein, ganz davon abhängig wieviel man weg nimmt oder hinzugibt.
