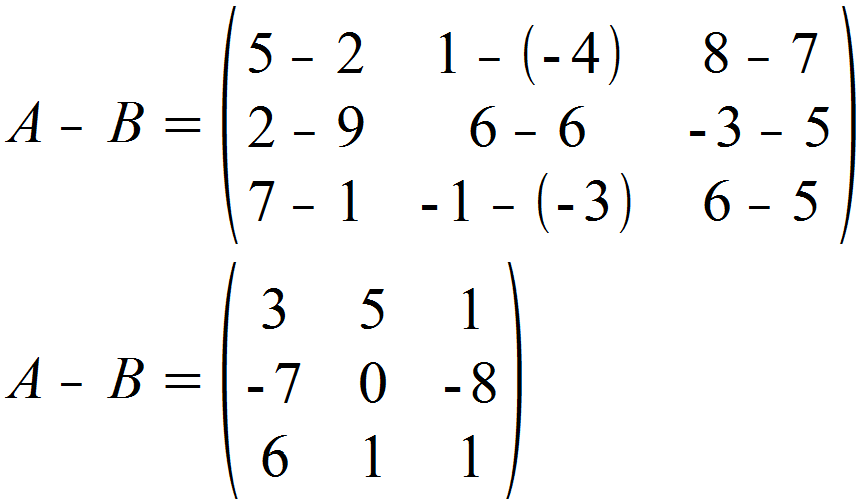Addition und Subtraktion

Generell lassen sich Matrizen nur addieren und subtrahieren, wenn ihre jeweilige Anzahl an Zeilen und Spalten übereinstimmt. Wir verfahren hier beispielhaft anhand der beiden (2,3)-Matrizen A und B, die wie folgt definiert sind:

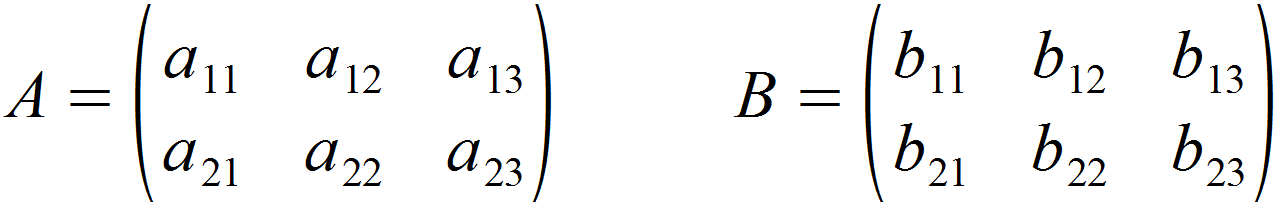
Für die Addition nehmen wir das jeweilige Element der gleichen Zeile und Spalte aus beiden Ausgangsmatrizen und fügen deren Summe an gleicher Stelle in eine neue Matrix ein, die Summenmatrix genannt wird. Da der Rechenweg in Worten viel komplizierter klingt, als er letztenendes ist, hier die Vorgehensweise mit Variablen:

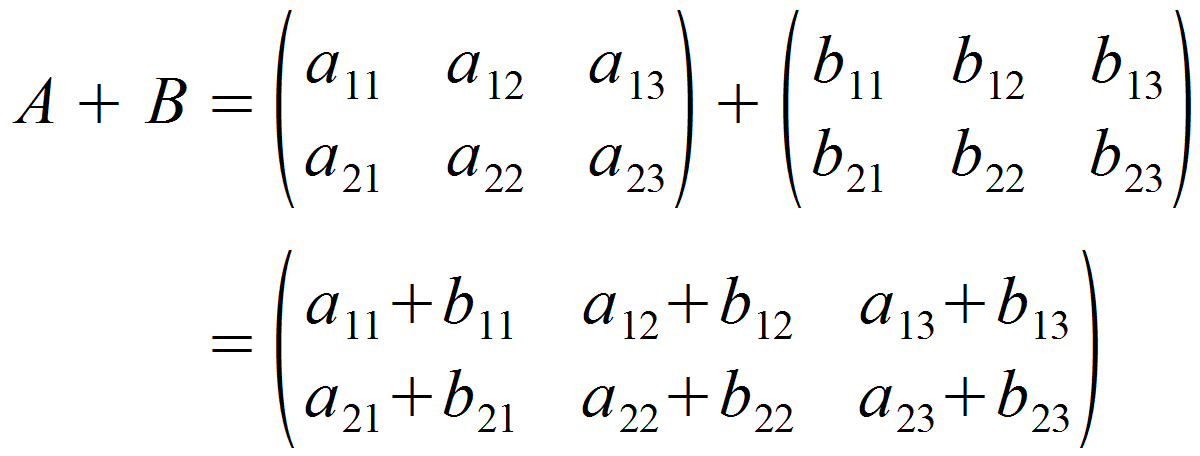
Die Subtraktion verläuft im Grunde analog. Wir nehmen wieder das jeweilige Element der gleichen Zeile und Spalte aus den Ausgangsmatrizen A und B, bilden davon allerdings die Differenz und fügen das Ergebnis in eine neue Matrix mit gleich vielen Zeilen und Spalten ein. Diese Matrix wird Differenzmatrix genannt.

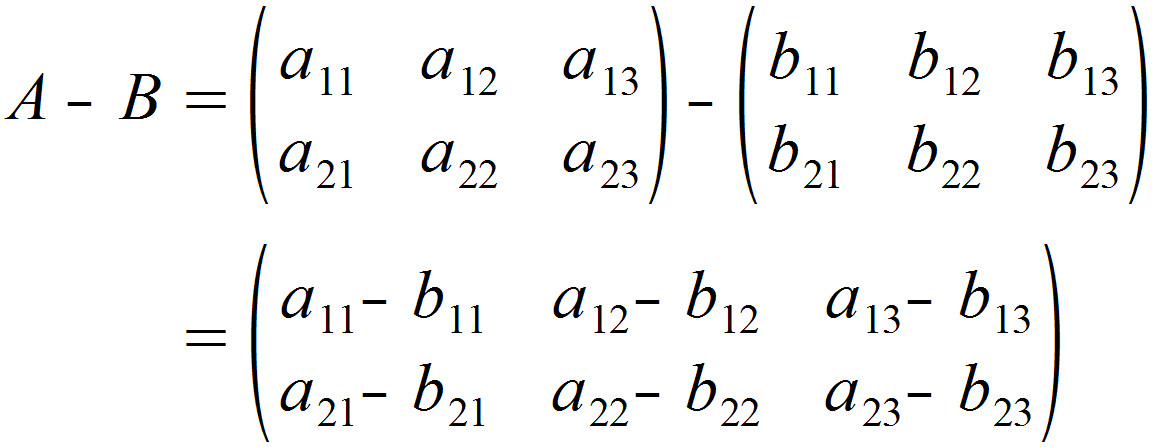
Für die Addition von Matrizen gilt das Kommutativ- und Assoziativgesetz. Es ist für das Ergebnis also nicht ausschlaggebend, in welcher Reihenfolge addiert wird.

 

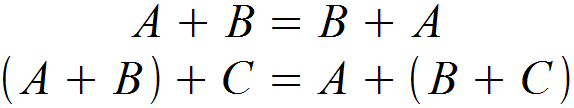
Gegenbeispiel

Die folgenden Matrizen A und B lassen sich nicht addieren. Warum ist das so?

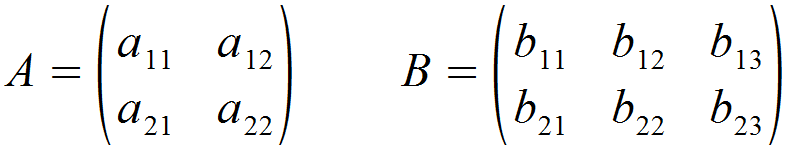
Die Matrix A ist eine (2,2)-Matrix, bei der Matrix B handelt es sich um eine (2,3)-Matrix. Da die Zeilen- und Spaltenzahl hier nicht übereinstimmt, ist weder eine Addition noch eine Subtraktion möglich.

Beispiele

Es soll die Summe und Differenz folgender Matrizen gebildet werden:

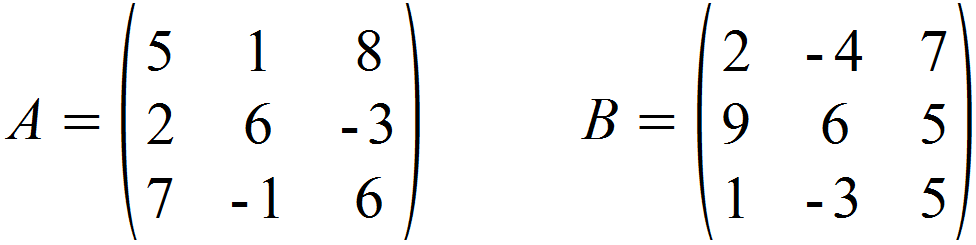
Addition

Wir gehen also wie oben beschrieben vor und addieren jeweils die Elemente der gleichen Position.

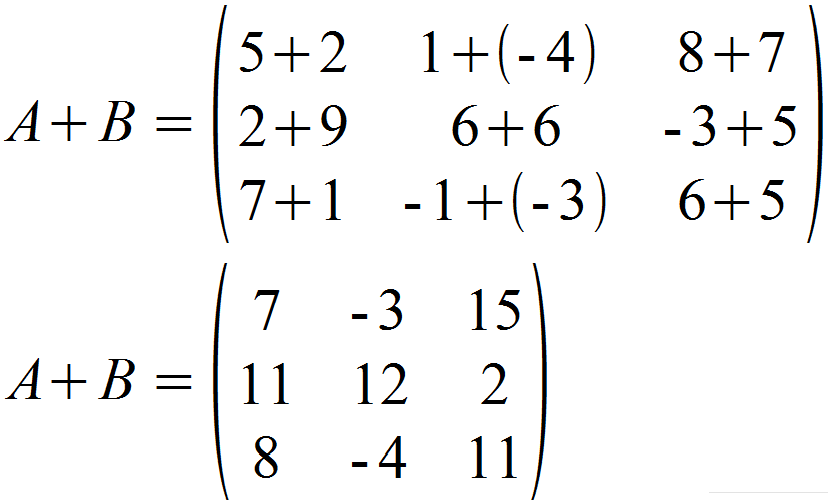
Subtraktion

Wir bilden die Differenz von Matrix A und B, indem wir die Elemente der gleichen Position in den Matrizen voneinander abziehen.