Spatprodukt
Wir befassen uns mit dem Thema Spatprodukt!
Aber was ist eigentlich das Spatprodukt?
Bevor wir das ganze mit einem Beispiel veranschaulichen, werden wir zuerst auf das inhaltliche zugehen damit wir es besser verstehen können.
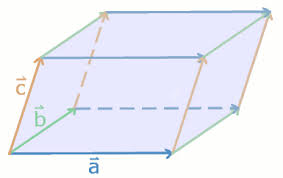
Stellt euch ein Prisma vor ( schiefes Prisma), das irgendwie in den Raum gestellt wurde. Wenn man drei Vektoren ( Achtung-Linear Unabhängig) gegeben hat, so spannen diese einen Körper, den sogenannten Spat auf!
Jede dieser Seiten hat unterschiedliche Richtungen ( Länge bzw auch Winkel). Jede dieser Richtungen müsst ihr als einzelne Vektoren betrachten- Vektor (a,b,c), die nicht der Nullvektor sind sondern einen Spat (Parallelvielfach) aufspannen.
Unser Lernvideo zu : Spatprodukt
Beispiele zum Spatprodukt
Wir berechnen jetzt gemeinsam Schritt für Schritt einen Beispiel
Berechnet werden soll das Spatprodukt mit den Vektoren
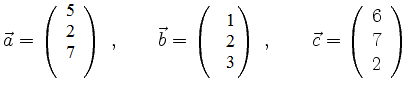
Schreibweise: [a⃗ ,b⃗ ,c⃗ ]:=a⃗ ⋅(b⃗ x c⃗ ):=b⃗ ⋅(a⃗ x c⃗ ):=c⃗ ⋅(a⃗ x b⃗ ).
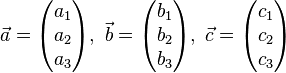
Am einfachsten ist das Spat zu berechnen mit der Regel von Sarrus. Diese besagt folgendes:
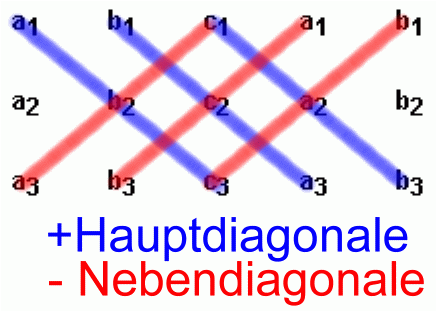
Berechnung nach dem Rechenschema
![]()
Auf unser Beispiel zurück zu führen; wird es folgendermaßen berechnet!
Wir setzen ein: (7*2*6)+(3*7*5)+(2*2*1) – (5*2*2)+(1*7*7)+(6*2*3)= 88
Durch das Ergebnis wissen wir, dass die Vektoren linear Unabhängig sind. Denn wäre es gleich Null, dann hätte wir den Fall, dass sie linear abhängig wären. Merken!
Hier noch einmal die kurze Zusammenfassung der Regel von Sarrus
⇒ Schreibt die ersten beiden Spalten der Determinante in ihrer Reihenfolge nochmal dahinter
⇒ bildet nun die Produkte aller Diagonalen (Achtung! immer 3 Komponenten)
⇒ Nun nach dem oben erklärten Schema berechen ( + Hauptdiagonale/ – Nebendiagonale)
Hauptdiagonale: von links oben nach rechts unten
Nebendiagonale: von links unten nach rechts oben
⇒ jetzt einfach den Wert berechnen
Mathe macht Spaß wenn man es kann! Und ihr könnt es auch
