Aufleiten Flächenberechnung
Das bestimmte Integral: Das bestimmte Integral einer Funktion f(x) von a bis b
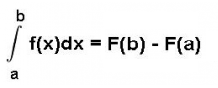
ist der Flächeninhalt der von der Funktionskurve und der x-Achse berandeten Fläche zwischen x =a und x= b. (Je nach Vorzeichen der Funktion und Integrationsrichtung trägt dieser Flächeninhalt ein positives oder negatives Vorzeichen)
Vorgehensweise
- Bestimme die Nullstellen um die Grenzen zu erhalten (falls diese nicht vorgegeben sind)
- Ist die Fläche stets oberhalb der x-Achse die bestimmt wird, kannst du ganz normal das Integral berechnen.
Merke: Wenn die Funktion im zu berechnendem Intervall einen Vorzeichenwechsel hat, ist ein Teil der Fläche unterhalb der x-Achse und eine Fläche oberhalb. Die Fläche unterhalb der x- Achse muss dann im Betrag genommen werden.
♦Das unbestimmte Integral stellt eine Menge von Funktionen dar, nicht etwa eine Zahlenwert wie beim bestimmten Integral!
Wie berechnet man eine Fläche?
⇒ schreibe das Integralzeichen hin
⇒ unterhalb und oberhalb des Integralzeichens stehen immer die untere und obere Flächengrenze
⇒ hinter dem Integralzeichen [im eigentliche Integral] stehen immer die obere und untere Funktion, die die Fläche begrenzen [es sind immer zwei Funktionen, auch wenn eine der Funktionen immer die x-Achse ist!]
⇒ zu allerletzt kommt das „dx“ [ohne wichtige Bedeutung]
Beispiel
Gegeben haben wir die folgende Funktion f(x) = -x2 + 5 mit dem Intervall [-2, 2]. Gesucht ist der Flächeninhalt.
Wir bestimmen zuerst die Stammfunktion: ∫f(x)dx= -x3/3 +5x
Da wir schon die Intervalle gegeben haben, können wir nun die Fläche berechnen
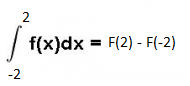
⇒ ( -8/3 +10) – ( 8/3-10)
⇒ -16/3 +20
⇒ 44/3 ≙ 14,67 LE
Die gesuchte Fläche beträgt also 14,67 LE ( Längeneinheiten)
