Bedingte Wahrscheinlichkeit
Was ist die Bedingte Wahrscheinlichkeit?
- Die bedingte Wahrscheinlichkeit beschreibt, wie hoch die Wahrscheinlichkeit ist, dass ein Ereignis B unter der Bedingung eintritt, dass ein anderes Ereignis A bereits eingetreten ist. Dies wird als P(A | B) geschrieben als „die bedingte Wahrscheinlichkeit von A, vorausgesetzt B“ gelesen.
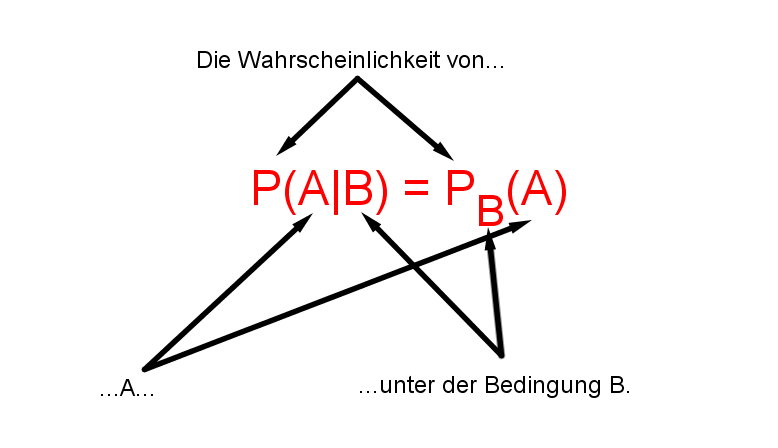
Mathematische Definition der Schreibweise
Der senkrechte Strich wird als „unter der Bedingung“ gelesen. Das Ereignis zu der rechten Seite des senkrechten Stiches (in diesem Fall B) ist das, von dem wir wissen, dass es eingetreten ist.
Die Formel für die bedingte Wahrscheinlichkeit lässt sich durch den Multiplikationssatz herleiten.
⇒Multiplikationssatz 
Sind A und B zwei unabhängige Ereignisse, dann ist die bedingte Wahrscheinlichkeit, dass Ereignis A eintritt, vorausgesetzt, dass B eintreten wird, gleich P(B).
Einzelne Definitionen und deren Bedeutung
PB(A) = bezeichnet die Wahrscheinlichkeit von A unter der Bedingung B ; d.h man weiß bereits sicher, dass B zutrifft bzw. eingetreten ist, aber bezüglich A weiß man es nicht und fragt nach der Wahrscheinlichkeit von A.
PA(B)= bezeichnet die Wahrscheinlichkeit von B unter der Bedingung A ; d.h. man weiß bereits sicher, dass A zutrifft bzw. eingetreten ist, aber bezüglich B weiß man es nicht und fragt nach der Wahrscheinlichkeit von B.
P( A ∩ B) = bezeichnet die Wahrscheinlichkeit des Ereignisses „A und zugleich B“ ; d.h. man hat keine zusätzlichen Informationen und fragt nach der Wahrscheinlichkeit, mit der A und B gemeinsam eintreten.
Beispiel 1
Eine Lehrerin schrieb mit ihrer Klasse zwei Klausuren. 55% bestanden beide Klausuren; 72% nur die erste. Wie viel Prozent derjenigen, die den ersten Test bestanden haben, haben auch den zweiten Test bestanden?
Dies ist eine Aufgabe der bedingten Wahrscheinlichkeit, da die Wahrscheinlichkeit derjenigen, die die zweite Klausur bestanden haben, gefragt ist, unter der Vorraussetzung, dass die erste bestanden wurde.
Beispiel 2
Wir haben 10 Murmeln, 4 rote und 6 blaue; wir nehmen wahllos zwei heraus. Nun definieren wir die Ereignisse A als „die erste Murmel ist rot“ und B als „die zweite Murmel ist rot“. Wie groß ist die Wahrscheinlichkeit, dass beide Murmeln rot sind P(A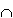 
B)?
Weil wir die Murmeln nacheinander herausnehmen können, ist die Wahrscheinlichkeit, dass die erste Murmel rot ist 4/10. Zwei rote Murmeln zu bekommen, kann als die bedingte Wahrscheinlichkeit, eine zweite rote Murmel zu bekommen P(B|A) – wenn gegeben ist, dass die erste rot ist -, angesehen werden. Nach der Entfernung der ersten Murmel, hat sich der Probenraum verändert: Wir haben nun 3 rote und 6 blaue Murmeln, also ist die Wahrscheinlichkeit eine rote Murmel zu bekommen nun P(B|A) = 3/9.
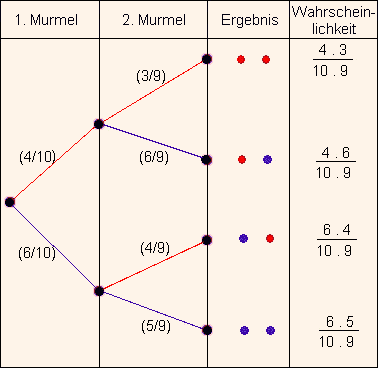
P(A 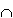B) = P(A) . P(B|A) = 4/10 * 3/9 = 2/15. Die Berechnung der Wahrscheinlichkeiten von Schnittmengen kann in einem Baumdiagramm dargestellt werden:
Unser Lernvideo zu : Bedingte Wahrscheinlichkeit
Wie sieht das Baumdiagramm aus?
jede bedingte Wahrscheinlichkeit könnt ihr auch an einem Baumdiagramm dargestellt werden.
So würde ein Baumdiagramm aussehen
