Bestimmtes Integral

Wir sind im vorherigen Artikel schon mit unbestimmten Integralen in Berührung gekommen. Das Ergebnis eines Integrals lässt sich als Fläche zwischen dem Graphen der Funktion, der x-Achse und den begrenzenden Parallelen zur y-Achse deuten.

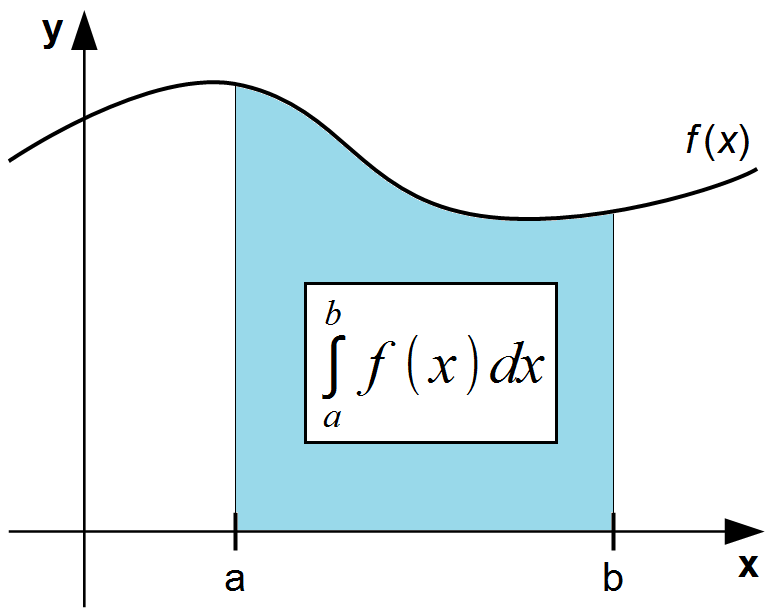
Um ebendiese Parallelen zur y-Achse zu kennen, sind die jeweiligen Punkte auf der x-Achse nötig. Sie werden untere und obere Integrationsgrenzen genannt und finden sich als a und b in der Darstellung des bestimmten Integrals wieder. Der Bereich zwischen a und b wird auch als Intervall [a;b] bezeichnet.

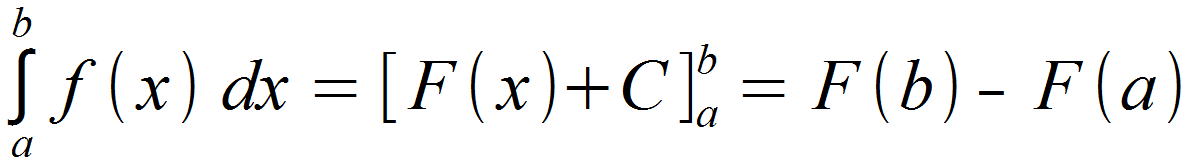
Man schreibt also das Integralzeichen ∫ mit der unteren Integrationsgrenze a darunter und der oberen Integrationsgrenze b darüber, gefolgt von der betrachteten Funktion sowie der Kennzeichnung, nach welcher Variable integriert wird. Im Regelfall ist dies die Variable x, also wird dx hinzugefügt.

Das Resultat ist die Differenz von F (b) und F (a), also der oberen und unteren Integrationsgrenzen eingesetzt in die Stammfunktion von f (x). Wie die Stammfunktion gebildet wird, haben wir bereits im vorherigen Artikel gelernt. Die Integrationskonstante C kürzt sich am Ende glücklicherweise raus und wir erhalten einen konkreten Zahlenwert als Ergebnis.

Unser Lernvideo zu : Bestimmtes Integral