Binomische Formeln
Die binomischen Formeln sind drei besonders wichtige Formeln, welche einem oft begegnen.
Zwar kennen wir schon alle Regeln um diese Formeln zu lösen und man kann sie sich auch relativ einfach herleiten, trotzdem wollen wir hier noch einmal alle drei binomischen Formeln erklären.
Aber eigentlich braucht ihr die Formeln gar nicht, wenn ihr das Rechnen mit den Klammern beherrscht. Ihr werdet sehen, die binomischen Formeln ergeben sich von ganz allein aus den allgemeingültigen Rechengesetzen. Von daher ist es ratsam, sich zunächst noch einmal mit den Klammern zu beschäftigen
Unser Lernvideo zu : Binomische Formeln
Erste binomische Formel
Könnt ihr Klammern bereits ausmultiplizieren? Dann wird euch diese Formel keinerlei Probleme mehr bereiten. Mit der Herleitung wollen wir euch den eigentlichen Ursprung dieses Gesetztes nur noch einmal verdeutlichen.
Die erste binomische Formel lautet:
![]()
Wir leiten diese noch einmal Schritt für Schritt her. Zunächst einmal lösen wir das Quadrat auf und schreiben die beiden Faktoren hintereinander:
![]()
Diesen Term multiplizieren wir nun mit Hilfe des Distributivgesetzes aus. Dabei multiplizieren wir die Teile der ersten Klammer mit den Teilen der zweiten.
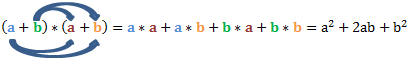
Beispiel 1
![]()
Wenn wir dieses Beispiel haben und die Klammer auflösen wollen, müssen wir die erste binomische Formel anwenden. Am besten können wir sie uns einfach merken und können dann sofort das Ergebnis notieren. In diesem Fall wird a zu x und b zu 5:
![]()
Damit sind wir bereits fertig. Weiter kann man das Ergebnis nicht zusammenfassen.
Beispiel 2
Natürlich kann man die binomische Formel auch andersrum anwenden. Mit der binomischen Formel kann man zum Beispiel folgenden Ausdruck zusammenfassen:
![]()
Wir müssen hierbei ein bisschen Aufpassen, da man nicht alle Terme dieser Art zusammenfassen kann. Wir müssen zunächst prüfen ob es sich tatsächlich um die erste binomische Formel handelt. Das a² am Anfang deutet natürlich schon einmal darauf hin. Wir vergleichen unseren Term mit der ersten binomischen Formel:
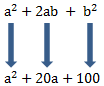
Die 20a müssten den 2ab entsprechen und die 100 müssen b² entsprechen. Wir müssen nun unser b berechnen. Wir wissen das 2ab = 20a ist.
![]()
Wir wollen b herausfinden. Deshalb formen wir die Gleichung nach b um. Wir teilen im ersten Schritt durch a. Dies dürfen wir hier tun, weil a nicht die gesuchte Variable ist. Wir können diese also kürzen.
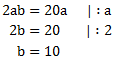
b ist also gleich 10. Wir überprüfen dies mit dem letzten Term der binomischen Gleichung. b² müsste nun 100 entsprechen:
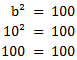
Wir sehen, dass diese Bedingung erfüllt ist. Damit können wir den Ausdruck mithilfe der binomischen Formel zusammenfassen. a ist dabei gleich a und b ist gleich 10.
![]()
Zweite binomische Formel
Die zweite binomische Formel sieht ähnlich aus wie die erste. Der einzige Unterschied ist, dass hier subtrahiert wird.
![]()
Auch diese Formel leiten wir noch einmal Schritt für Schritt her. Dabei ist das Vorgehen dasselbe wie bei der ersten binomischen Formel. Der erste Schritt ist wieder das Quadrat durch eine Multiplikation zu ersetzen.
![]()
Es folgt wieder das Ausmultiplizieren:
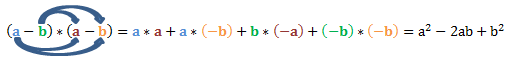
Hier müssen wir uns daran erinnern, dass Minus mal Plus Minus ergibt und das Minus mal Minus Plus ergibt.
Beispiel 1
![]()
Wir können hier einfach die oben hergeleitete Formel anwenden. a wird dabei zu x und b wird zu 5. Dadurch erhalten wir:
![]()
Beispiel 2
Auch die zweite binomische Formel kann man in bestimmten Situationen andersherum anwenden. Es ist aber auch hier wichtig zu überprüfen ob es sich tatsächlich um die binomische Formel handelt.
![]()
Diesem Term vergleichen wir mit ![]() . Aufgrund des Minuszeichens wissen wir, dass es sich um die zweite Binomische Formel handeln muss.
. Aufgrund des Minuszeichens wissen wir, dass es sich um die zweite Binomische Formel handeln muss.
Wir vergleichen unseren Term mit dem der binomischen Formel:
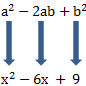
Wir sehen, dass a hier x entspricht. 2ab ist in unserem Beispiel 6x und b² ist hier gleich 9. Wir Schreiben dies einmal auf:
![]()
Im mittleren Teil gilt:
![]()
Da wir schon wissen, das a = x ist, können wir für a x einsetzen:
![]()
Wir kommen im zweiten Teil also auf b = 3. Nun betrachten wir noch den dritten Teil:
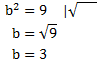
Das Wurzelzeichen hinter dem senkrechten Stricht bedeutet hier, dass wir auf beiden Seiten die Wurzel ziehen.
Wir kommen auch hier auf das Ergebnis b = 3. Die Bedingung für die binomische Formel ist also erfüllt. Wir dürfen deshalb schreiben:
![]()
Dritte binomische Formel
Die dritte binomische Formel sieht etwas anders aus. Hier wird in einer Klammer subtrahier und in der anderen addiert. Wie rum die beiden Klammer stehen, ist dabei wegen des Kommutativgesetzes nicht von Bedeutung.
Eigentlich können wir mit dieser Formel zwei Klammern ausmultiplizieren. Werft einen Blick auf die Herleitung und die Rechenwege, um diese mit natürlichen Zahlen ausrechnen zu können
![]()
Die Herleitung sieht folgendermaßen aus:
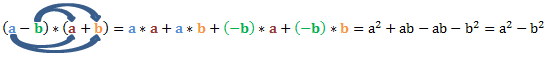
Beispiel 1
![]()
In diesem Beispiel sehen wir recht schnell, dass a hier x entspricht und b hier gleich 4 ist:
![]()
Beispiel 2
Bei der dritten binomischen Formel ist auch die Anwendung andersherum relativ einfach. Wir haben folgenden Term:
![]()
Durch die Betrachtung der Herleitung wissen wir:
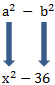
Daraus ergibt sich:
![]()
und:
![]()
Die binomische Formel lautet also:
![]()
Binomische Formeln für Fortgeschrittene
Erst wenn ihr die oben genannten Formeln mit den Exponenten 2 richtig lösen könnt, ist es so weit – einen Blick auf die höheren Exponenten zu werfen, wie zum Beispiel 3 oder 4. Starten wir mit dem Exponenten 3, treffen wir auf die folgende Formel:
( a + b )3 = a3 + 3a2b + 3ab2 + b3
( 3 + 5 )3 =33 + 3 · 3 · 52 + 3 · 32 · 5 + 53
( 3 + 5 )3 = 512
Wollen wir die binomischen Formeln rückwärts anwenden, dann faktorisieren wir, indem wir die Formeln ausklammern.


